Beyond news contents: the role of social context for fake news detection
Today we’re looking at a more general fake news problem: detecting fake news that is being spread on a social network. This is a summary of a recent paper which demonstrates why we should also look at the social context: the publishers and the users spreading the information!
Beyond news contents: the role of social context for fake news detection Shu et al., WSDM’19
Today we’re looking at a more general fake news problem: detecting fake news that is being spread on a social network. Forgetting the computer science angle for a minute, it seems intuitive to me that some important factors here might be:
- what is being said (the content of the news), and perhaps how it is being said (although fake news can be deliberately written to mislead users by mimicking true news)
- where it was published (the credibility / authority of the source publication). For example, something in the Financial Times is more likely to be true than something in The Onion!
- who is spreading the news (the credibility of the user accounts retweeting it for example – are they bots??)
Therefore I’m a little surprised to read in the introduction that:
The majority of existing detection algorithms focus on finding clues from the news content, which are generally not effective because fake news is often intentionally written to mislead users by mimicking true news.
(The related work section does however discuss several works that include social context.).
So instead of just looking at the content, we should also look at the social context: the publishers and the users spreading the information! The fake news detection system developed in this paper, TriFN considers tri-relationships between news pieces, publishers, and social network users.
… we are to our best knowledge the first to classify fake news by learning the effective news features through the tri-relationship embedding among publishers, news contents, and social engagements.

And guess what, considering publishers and users does indeed turn out to improve fake news detection!
Inputs
We have publishers,
social network users, and
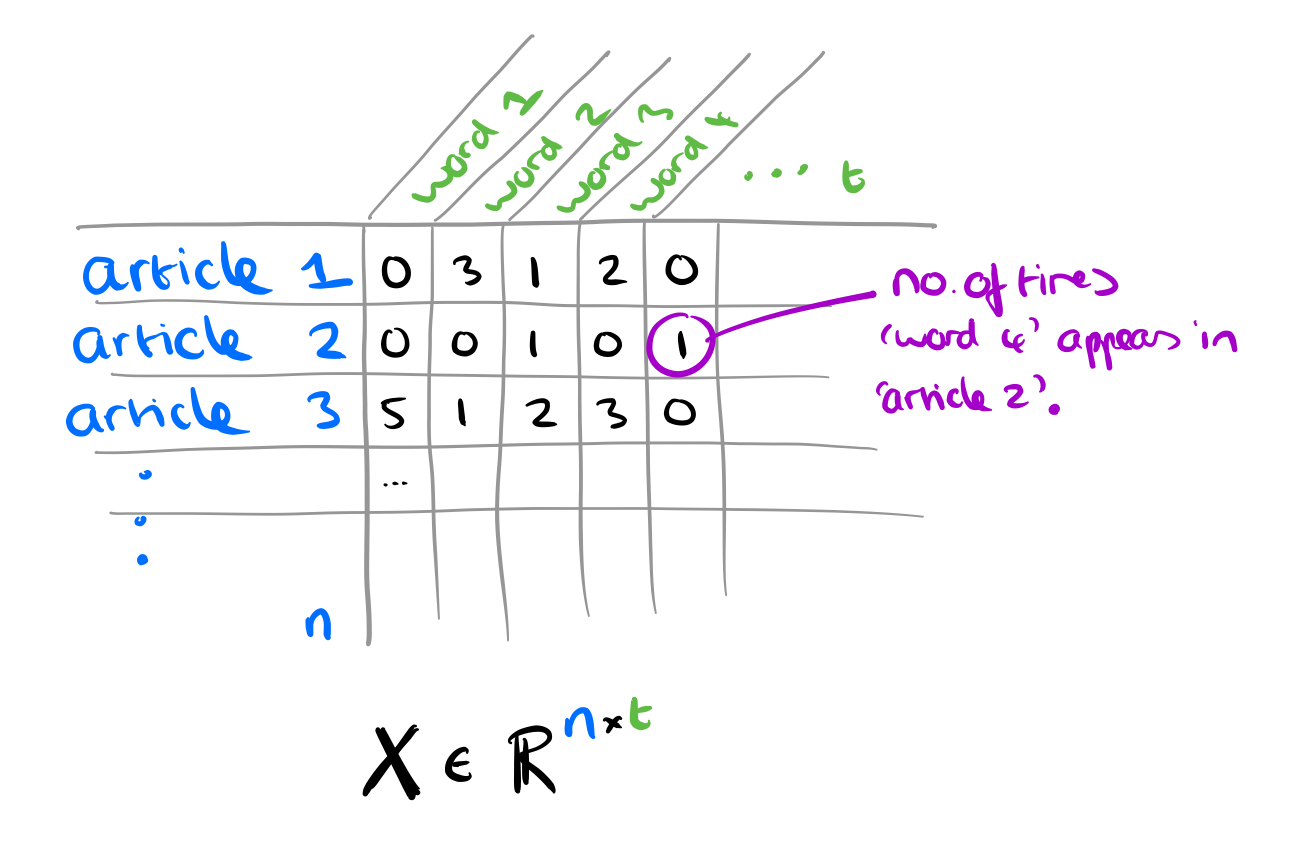
news articles. Using a vocabulary of t words, we can compute an
bag-of-word feature matrix.
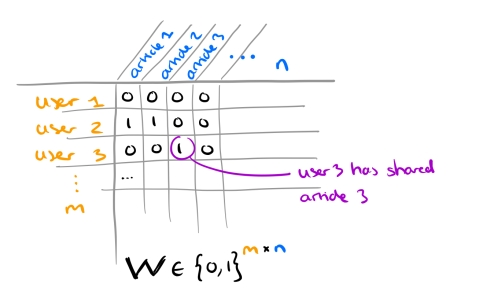
For the m users, we can have an m x m adjacency matrix , where
is 1 if i and j are friends, and 0 otherwise.
We also know which users have shared which news pieces, this is encoded in a matrix .
The matrix similarly encodes which publishers have published which news pieces.
For some publishers, we can know their partisan bias. In this work, bias ratings from mediabiasfactcheck.com are used, taking just the ‘Left-Bias’, ‘Least-Bias’ (neutral) and ‘Right-Bias’ values (ignoring the intermediate left-center and right-center values) and encoding these as -1, 0, and 1 respectively in a publisher partisan label vector, . Not every publisher will have a bias rating available. We’d like to put ‘-’ in the entry for that publisher in
but since we can’t do that, the separate vector
encodes whether or not we have a bias rating available for publisher p.
There’s one last thing at our disposal: a labelled dataset for news articles telling us whether they are fake or not. (Here we have just the news article content, not the social context).
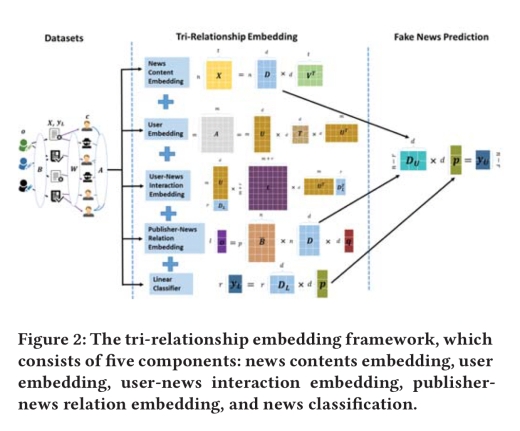
The Tri-relationship embedding framework
TriFN takes all of those inputs and combines them with a fake news binary classifier. Given lots of users and lots of news articles, we can expect some of the raw inputs to be pretty big, so the authors make heavy use of dimensionality reduction using non-negative matrix factorisation to learn latent space embeddings (more on that in a minute!) TriFN combines:
- A news content embedding
- A user embedding
- A user-news interaction embedding
- A publisher-news interaction embedding, and
- The prediction made by a linear classifier trained on the labelled fake news dataset
Pictorially it looks like this (with apologies for the poor resolution, which is an artefact of the original):
News content embedding
Let’s take a closer look at non-negative matrix factorisation (NMF) to see how this works to reduce dimensionality. Remember the bag-of-words sketch for news articles? That’s an n x t matrix where n is the number of news articles and t is the number of words in the vocabulary. NMF tries to learn a latent embedding that captures the information in the matrix in a much smaller space. In the general form NMF seeks to factor a (non-negative) matrix M into the product of two (non-negative) matrices W and H (or D and V as used in this paper). How does that help us? We can pick some dimension d (controlling the size of the latent space) and break down the matrix into a d-dimension representation of news articles
, and a d-dimension representation of words in the vocabulary,
. That means that
has shape
and so
ends up with the desired shape
. Once we’ve learned a good representation of news articles,
we can use those as the news content embeddings within TriFN.
We’d like to get as close to
as we can, and at the same time keep
and
‘sensible’ to avoid over-fitting. We can do that with a regularisation term. So the overall optimisation problem looks like this:

User embedding
For the user embedding there’s a similar application of NMF, but in this case we’re splitting the adjacency matrix into a user latent matrix
, and a user correlation matrix
. So in this case we’re using NMF to learn
which has shape mxd . dxd . dxm, resulting in the desired mxm shape. There’s also a user-user relation matrix
which controls the contribution of
. The basic idea is that any given user will only share a small fraction of news articles, so a positive case (having shared an article) should have more weight than a negative case (not having shared).
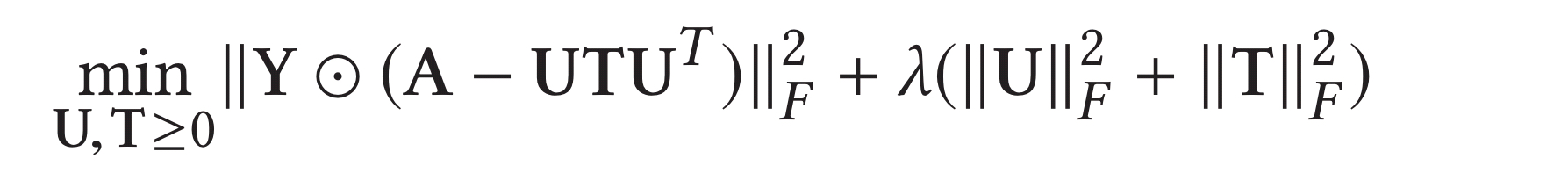
User-news interaction embedding
For the user-news interaction embedding we want to capture the relationship between user features and the labels of news items. The intuition is that users with low credibility are more likely to spread fake news. So how do we get user credibility? Following ‘Measuring user credibility in social media’ the authors base this on similarity to other users. First users are clustered into groups such that members of the same cluster all tend to share the same news stories. Then each cluster is given a credibility score based on its relative size. Users take on the credibility score of the cluster they belong to. It all seems rather vulnerable to the creation of large numbers of fake bot accounts that collaborate to spread fake news if you ask me. Nevertheless, assuming we have reliable credibility scores then we want to set things up such that the latent features of high-credibility users are close to true news, and the latent features of low-credibility users are close to fake news.
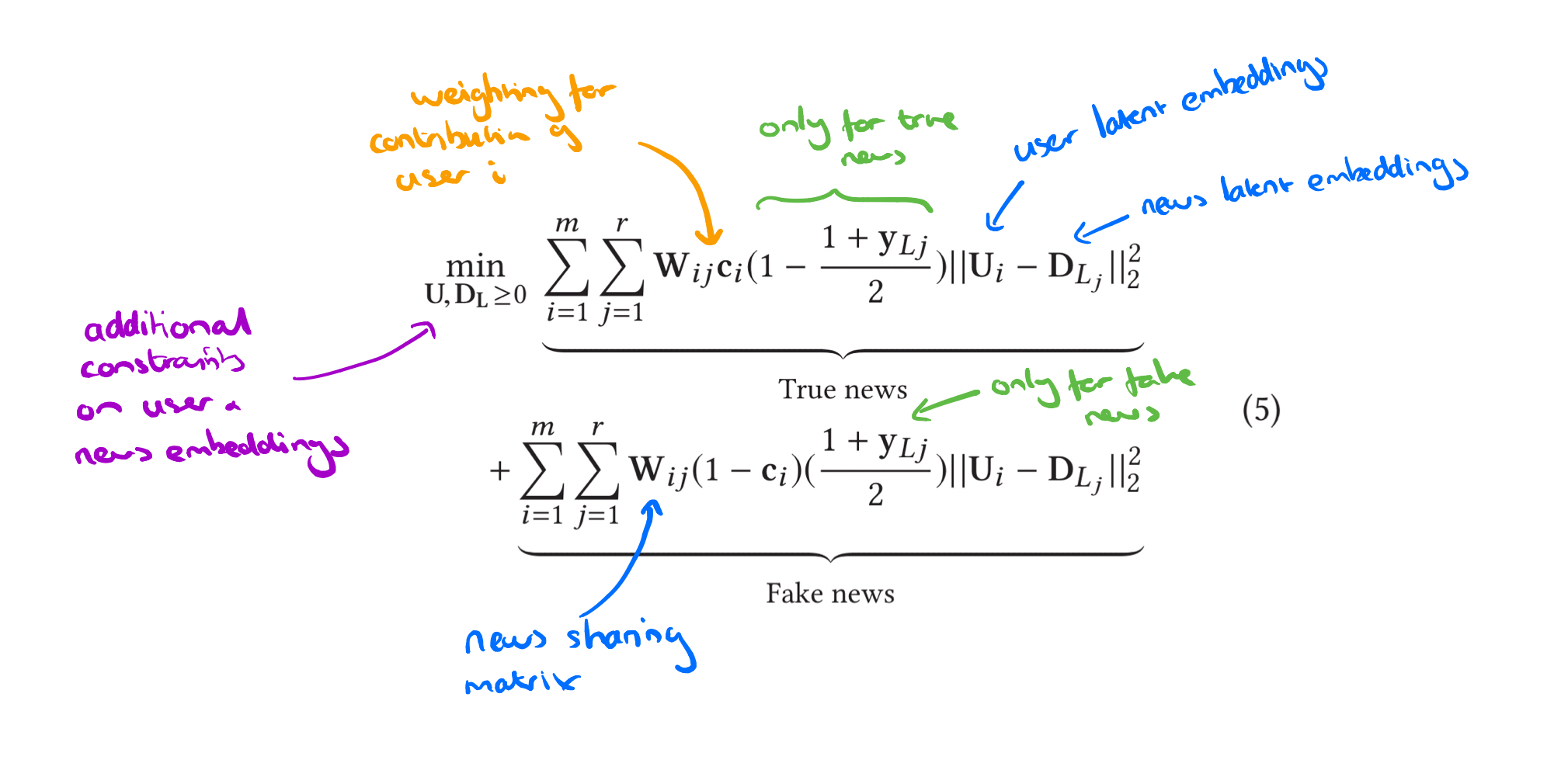
Publisher-news embeddings
Recall we have the matrix encoding which publishers have published which news pieces. Let
be the normalised version of the same. We want to find
, a weighting matrix mapping news publisher’s latent features to the corresponding partisan label vector
. It looks like this:
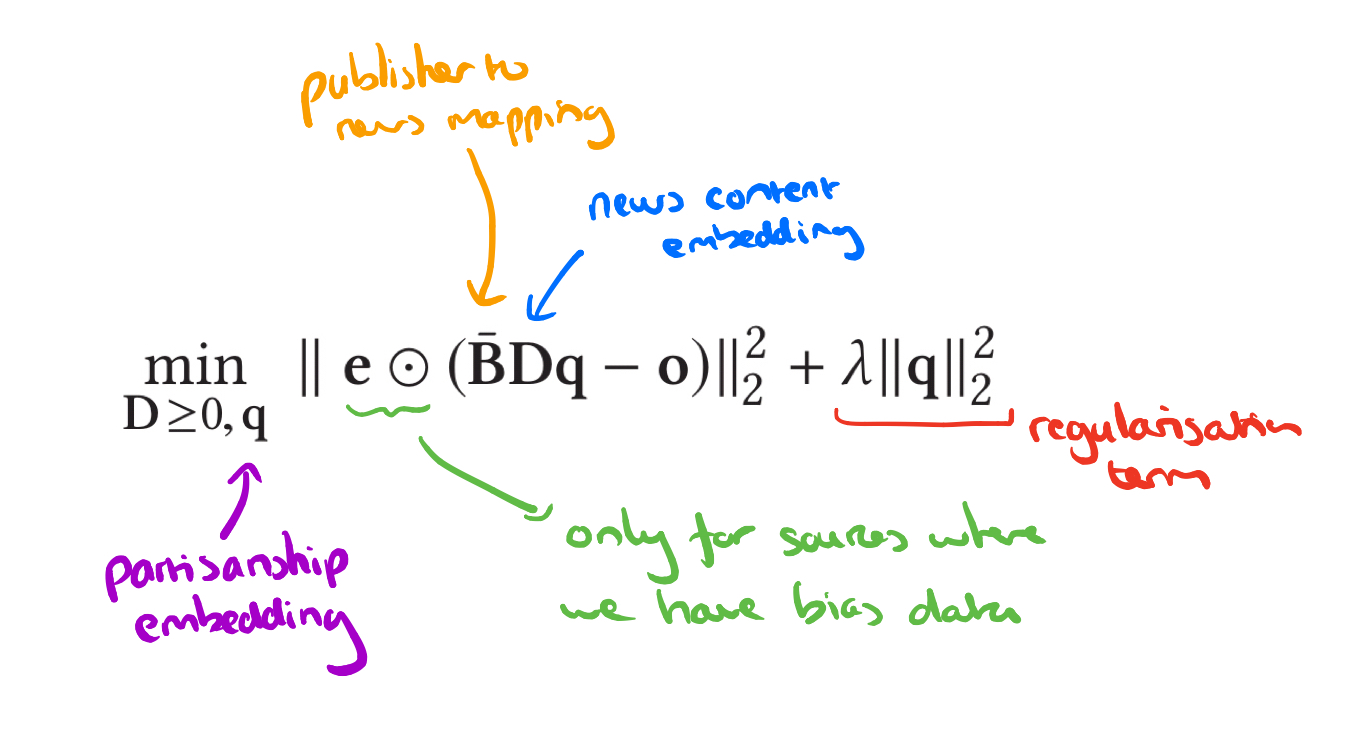
Semi-supervised linear classifier
Using the labelled data available, we also learn a weighting matrix mapping news latent features to fake news labels.
Putting it all together
The overall objective becomes to find matrices using a weighted combination of each of the above embedding formulae, and a regularisation term combining all of the learned matrices.
It looks like this:
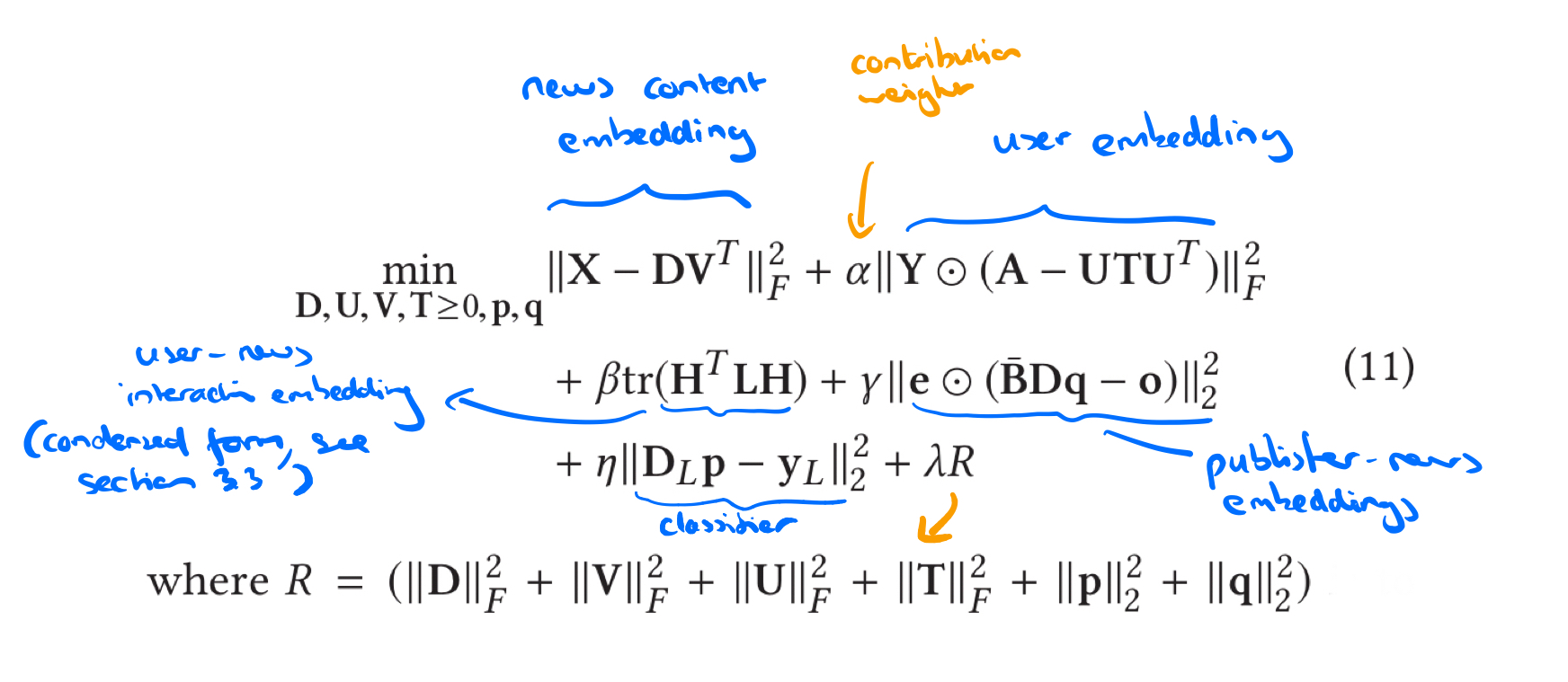
and it’s trained like this:

Evaluation
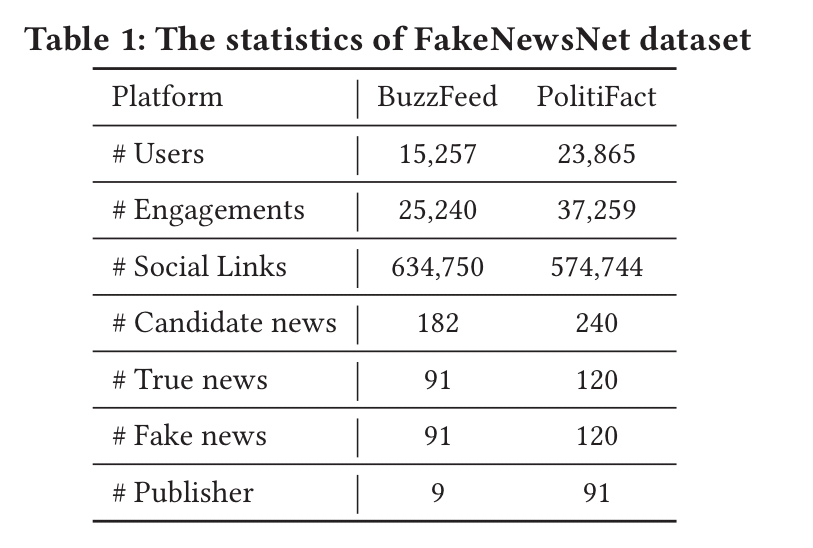
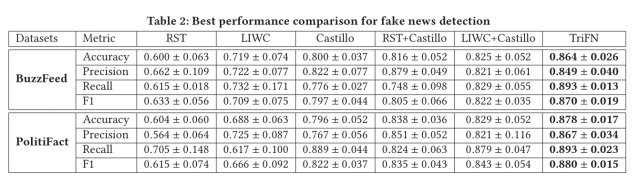
TriFN is evaluated against several state of the art fake news detection methods using the FakeNewsNet BuzzFeed and PolitiFact datasets.
It gives the best performance on both of them:
(Enlarge)
Original. Reposted with permission.
Related:
- A Quick Guide to Fake News Detection on Social Media
- Beware of Two Data Obfuscation Tactics
- It’s Getting Hot In Here: Data Science vs Fake News
