Computational Complexity of Deep Learning: Solution Approaches
Why has deep learning been so successful? What is the fundamental reason that deep learning can learn from big data? Why cannot traditional ML learn from the large data sets that are now available for different tasks as efficiently as deep learning can?
By Dr. Vijay Srinivas Agneeswaran,
This blog was inspired by a podcast on “Why you should optimize your deep learning inference platform” hosted by Ben Lorica on the Data Exchange.
Deep learning has been remarkably successful in a wide range of tasks such as being part of the Go champion defeating machine (AlphaGo defeated the world Go champion Lee Sedol) and as the single driver for a number of advances in recent months in areas such as computer vision, speech processing, language translation etc.
Why has deep learning been so successful? What is the fundamental reason that deep learning can learn from big data? Why cannot traditional ML learn from the large data sets that are now available for different tasks as efficiently as deep learning can? These questions can be answered by understanding the learnability of deep learning — otherwise known as Vapnik-Chervonenkis dimension, illustrated beautifully by the curve in figure 1 [1]. The curve captures the performance of traditional ML and DL VS the amount of data used to train the models. It can be observed that when data sets are small, the traditional ML has better performance compared to DL, but as the data sets move into the big data zone, the DL’s performance keeps increasing, almost exponentially. This is the reason we are seeing such a significant performance gain for deep learning on specific tasks, where there is large, labeled data sets available for training (image classification is the classic example).

Figure 1: Source Credit [1].
One of the trends observed in the recent past is that deep neural networks are being overparametrized, which means that the number of parameters is much larger than the number of available data points for training. It has been proven that for training an overparametrized neural network, certain characteristics allow globally optimal models to be found efficiently by local heuristics and quadratic activations [2]. An Illustration of overparametrized nets is the state-of-art image recognition system NosiyStudent [3], which has about 480M parameters or by Microsoft’s Turing NLG, which had 17 billion parameters. This has been taken to an extreme by GPT3 from OpenAI, which has 175B parameters. Though some researchers like Gary Marcus have shown that GPT3 can generate natural language, but quite senseless — this is a separate topic for further research.
Computational requirement of overparametrized nets is proportional to the product of number of data points and number of parameters (and given that in an overparametrized setting, the number of parameters required grows with the number of data points) — this essentially implies that the computational requirement to train overparametrized deep learning is quadratic with the number of data points. The computational requirement of commonly used deep learning models is quantified in the graph in figure 2, courtesy of [4]. As can be observed from the graph, the best performing pre-trained architectures are those which have very high computational complexity (like NASNet-A-Large), at the extreme right in the figure. It should also be borne in mind that they are not the ones with maximal model complexity (as is evidenced by the size of the bubble). Another important observation is that almost all of the models are capable of achieving real-time or super real-time performance on a high end GPU, which may imply that having GPUs solves computational problems.

Figure 2: Source Credit [4]
The point that we are trying to make is that while GPUs solved some of the computational complexity and helped in adoption of deep learning, the amount of computing power actually used in state-of-art systems like AlexNet or ResNext-101 grew even faster.
From an energy perspective also, the carbon footprint of deep learning is enormous. As can be seen from the table in figure 3 from [5], the cost of training common NLP models such as BERT or Transformers is quite high, with Network Architecture Search (NAS), a way to tune the hyper-parameters of a model and arrive at the optimal model, being the highest burden on the environment. Compare this cost in column CO2e with the cost of air travel for 1 passenger to go from NY to SFO costing 1984 on the same scale.

Figure 3: Source Credit [5]
Solutions
GPUs have been at the forefront of the deep learning revolution, starting from the foundational paper by Hinton, when they tackled the ImageNet challenge using deep learning on GPUs [6] and many other deep learning wins in the last few years in various challenges across computer vision, language translation and speech processing. Google also came up with the specialized hardware for accelerating deep learning inferencing, known as Tensor Processing Units (TPUs) [7], which have now been made available in the Google cloud. TPUs achieve significant speed ups for deep learning and also consume much lesser power. Nvidia also came up with their own specialized hardware for accelerating deep learning known as the Xavier processors, which can deliver 30 trillion operations per second consuming only 30 watts of power. Since these specializations are facing diminishing returns, there are other hardware advances that are being explored including quantum computing. A interesting work is in [8], where the authors show how complex neural architectures with intra-layer interconnections can be implemented on HPC (like ORNL’s Titan supercomputer), neuromorphic computing (for spiked neural networks) and Quantum computing (network of Boltzmann machines).
The second broad body of work tries to reduce the computational complexity of deep learning by sparsifying a trained neural network, so that it requires much lesser computation for inferencing. The three common approaches in this include pruning, low-rank compression and quantization. For instance, the work in [9] uses a low cost collaborative layer to accelerate each convolutional layer in the network. The technique of progressive shrinking used in the once-for-all network [10] is a generalized multi-dimensional pruning method. Another interesting effort in this direction is the BNNs (binary neural networks), which is one way to quantize the network. Low Rank Approximation (LRA) is a technique for replacing a large matrix multiplication with two or more smaller matrices to reduce the computational complexity. [11] Proposes Force Regularization to coordinate the deep learning filters to more correlated states, to achieve more efficient LRA.
The third body of work lies in finding small deep learning architectures, which are computationally more efficient. For instance, Neural Architecture Search (NAS) was originally proposed using reinforcement learning [12] to arrive at the best possible architecture (close to human crafted ones) by searching the possible space of hyper-parameters. The architecture so found is likely to perform efficiently for inferencing. However, it is not guaranteed to be the low energy model plus the whole search process itself is quite computationally intensive. ENAS was proposed to alleviate some of the issues in [13]– here the key improvement is to make the child models share parameters (weights) instead of training each child model from scratch. Another interesting approach to finding the smaller architectures is the lottery ticket hypothesis outlined in [14], which says finding such an ideal performing architecture is like winning a lottery ticket (close to having ideal initialization parameters) and describes one way to achieve the same. Another related method that helps in reducing model size of deep networks is “knowledge distillation” [15]. In this method, we first train a large model referred to as “teacher model”. Next, we train a smaller model, referred to as “student model”, which tries to mimic the behaviour of the teacher model. The student model does so by trying to replicate the outputs of specific layers of the teacher model along with the final loss.
Along similar lines, there is the thought process that deep learning may need to be enhanced in different ways to make it better for the real-world applications, especially from the perspective of human-like learning [16]. Recent efforts from both Google and Faceboook have attempted to add basic intuitive physics (like gravity, shapes etc.) into deep learning models. Differentiable Neural Computer (DNC) is a neural network augmented with random access read-write memory that maintains end-to-end differentiability, which has been applied to solving block puzzles and finding paths between nodes in a graph. Powering AlphaGo, the machine that beat a human champion in the game go, was a deep learning system augmented with model-based tree search [17], which is a classical AI building block. A recent start-up in this space is deci.AI, which has come up with a technology named as Automated Neural Architecture Construction (AutoNAC) to take as input an existing neural network and convert it into a much more computationally efficient network.
Another approach to evade the computational limits of deep learning would be to move to other, perhaps as yet undiscovered types of machine learning. For example, “expert” models can be computationally much more efficient, but their performance plateaus (Figure 4) [2] if the contributing factors can’t be explored and identified by those experts as efficiently as a flexible model. One example where such techniques are already outperforming deep learning models are those where engineering and physics knowledge can be more-directly applied: the recognition of known objects (e.g. vehicles) [18] [19]. The recent development of symbolic approaches to machine learning take this a step further, using symbolic methods to efficiently learn and apply “expert knowledge” in some sense, e.g. [20] which learns physics laws from data, or approaches [21] [22] which apply neuro-symbolic reasoning to scene understanding, reinforcement learning, and natural language processing tasks, building a high-level symbolic representation of the system in order to be able to understand and explore it more effectively with less data.
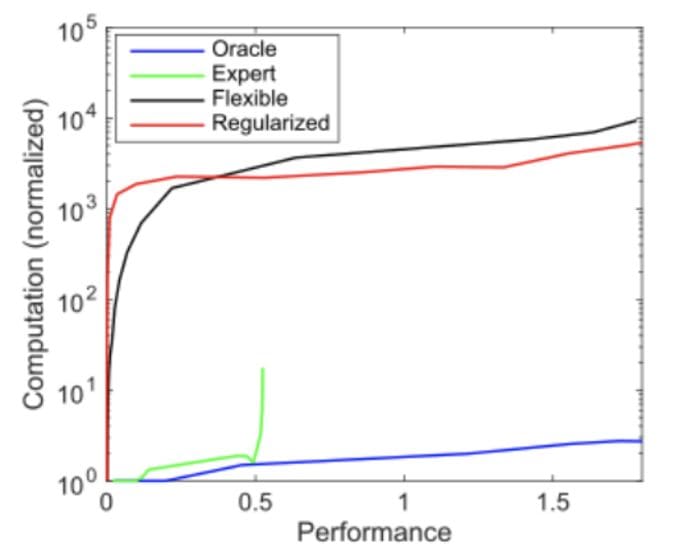
Figure 4: Source Credit [2]
References
[1] M. Alom, T. Taha, C. Yakopcic, S. Westberg, P. Sidike, M. Nasrin, M. Hasan, B. Van Essen, A. Awwal and V. Asari, A State-of-the-Art Survey on Deep Learning Theory and Architectures, vol. 8(3), Electronics, 2019, p. 292.
[2] N. C. Thompson, K. Greenewald, K. Lee and G. F. Manso, COmputational Limits of Deep Learning, vol. 4, MIT Initiative on the DIgital Economy Research Brief, 2020.
[3] Q. Xie, M.-T. Luong, E. Hovy and Q. V. Le, “Self-Training With Noisy Student Improves ImageNet Classification,” in IEEE Conference on Computer Vision and Pattern Recognition, Seattle, 2020.
[4] S. Bianco, R. Cadene, L. Celona and P. Napoletano, “Benchmark Analysis of Representative Deep Neural Network Architectures,” IEEE Access, vol. 6, pp. 64270–64277, 2018.
[5] E. Strubell, A. Ganesh and A. McCallum, “Energy and Policy Considerations for Deep Learning in NLP,” in In the 57th Annual Meeting of the Association for Computational Linguistics (ACL), Florence, Italy, 2019.
[6] A. Krizhevsky, l. Sutskever and G. E. Hinton., “ImageNet Classification with Deep Convolutional Neural Networks,” Communications of the ACM, vol. 60, no. 6, pp. 84–90, 2017.
[7] N. P. Jouppi and e. al, “In-Datacenter Performance Analysis of a Tensor Processing Unit,” in Proceedings of the 44th Annual International Symposium on Computer Architecture (ISCA ‘17), NY, 2017.
[8] T. E. Potok, C. Schuman, S. Young, R. Patton, F. Spedalieri, J. Liu, K.-T. Yao, G. Rose and G. Chakma, “A Study of Complex Deep Learning Networks on High-Performance, Neuromorphic, and Quantum Computers,” ACM Journal of Emerging Technologies in Computing Systems, vol. 14, no. 2, July 2018.
[9] X. Dong, J. Huang, Y. Yang and S. Yan, “More is Less: A More Complicated Network with Less Inference Complexity,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017.
[10] H. Cai, C. Gan, T. Wang, Z. Zhang and S. Han, “Once for All: Train One Network and Specialize it for Efficient Deployment,” in International Conference on Learning Representations (ICLR), 2020.
[11] Wei Wen et. al, “Coordinating Filters for Faster Deep Neural Networks,” in IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 2017.
[12] B. Zoph and Q. V. Le, “Neural Architecture Search with Reinforcement Learning,” in International Conference on Learning Representations, 2016.
[13] H. Pham, M. Y. Guan, B. Zoph, Q. V. Le and J. Dean, “Efficient Neural Architecture Search via Parameter Sharing,” in International Conference on Machine Learning (ICML), 2018.
[14] J. Frankle and M. Carbin, “The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks,” in International Conference on Learning Representations (ICLR), 2019.
[15] G. Hinton, O. Vinyals and J. Dean, “Distilling the Knowledge in a Neural Network,” in NIPS Deep Learning and Representation Learning Workshop , 2015.
[16] B. M. Lake, T. D. Ullman, J. B. T. Gershman and J. Samuel, “Building Machines That Learn and Think Like People,” Behavioural Brain Science, vol. 40, Nov 2017.
[17] David Silver et. al, “Mastering the game of Go with deep neural networks and tree search,” Nature, vol. 529, pp. 484–503, 2016.
[18] T. He and S. Soatto, “Mono3d+: Monocular 3d vehicle detection with two-scale 3d hypotheses and task priors,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2019.
[19] V. Tzoumas, P. Antonante and L. Carlone, “Outlier-robust spatial perception: Hardness, general-purpose algorithms, and guarantees,” in arXiv, stat.ML, 2019.
[20] S.-M. Udrescu and M. Tegmar, “Ai feynman: A physics-inspired method for symbolic regression,” Science Advances, vol. 6, no. 16, 2020.
[21] M. Asai and C. Muise., “Learning Neural-Symbolic Descriptive Planning Models via Cube-Space Priors: The Voyage Home (to STRIPS),” in International Joint Conference on Artificial Intelligence (IJCAI), 2020.
[22] K. Yi, J. Wu, C. Gan, A. Torralba, P. Kohli and J. Tenenbaum, “Neural-symbolic vqa: Disentangling reasoning from vision and language understanding,” in Advances in Neural Information Processing Systems (NIPS), 2018.
Tools
- https://quic.github.io/aimet-pages/index.html — see if this can be leveraged to optimize TensorFlow notebooks along with DeepSpeed for PyTorch notebooks.
- https://github.com/IntelLabs/distiller — auto compression framework — not sure if this can be explored for all types of models.
- https://github.com/forresti/SqueezeNet — one of the older frameworks — must see if this is current.
Bio: Dr. Vijay Srinivas Agneeswaran is leading data sciences foundations team and the element platform at Walmart Global Tech. He has a PhD from IIT Madras and 20+ years of R&D experience.
Original. Reposted with permission.
Related:
- Microsoft Research Trains Neural Networks to Understand What They Read
- 10 Real-Life Applications of Reinforcement Learning
- Know-How to Learn Machine Learning Algorithms Effectively
