An Overview of Logistic Regression

Many of you may be questioning if logistic regression be used for many independent variables as well??

The answer is yes, logistic regression can be used for as many independent variables as you want. However, be aware that you won’t be able to visualize the results in more than three dimensions.

Before these points, let's first discuss the logistic function aka the sigmoid function.

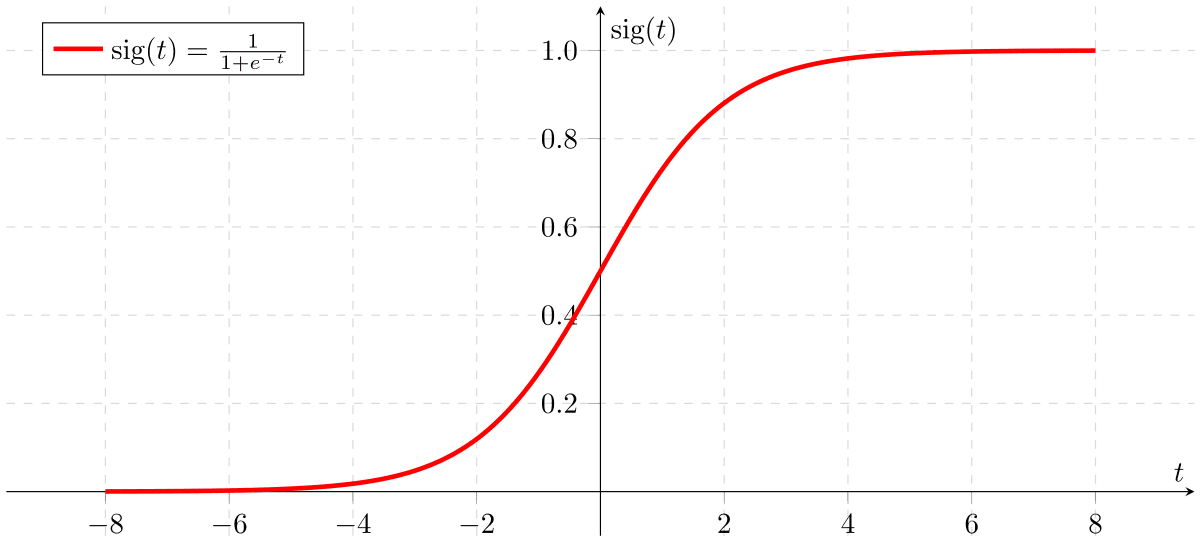
Sigmoid Function (from Figure 1)

 
Logistic regression is named for the function used at core of the method, the logistic function. It is also called the sigmoid function. It is used to describe properties of population growth in ecology, rising quickly and maxing out at the carrying capacity of the environment. It's a three shape curve that can take any value number and map it into a value between 0 and 1, but never exactly at those limits.

We can derive

Sigmoid Function = 1 / 1 + e^-value

where:

e = base of the natural logarithm

It is also used when we can't separate the data into classes by a linear boundary.

From the example:

p / 1 - p

where;

p = probability of an event

We can create formula from this

log p / 1 - p

It was also used in biological science in the early days. It was then used in many social science applications. It is used when the dependent variable is categorical.

Here is a simple model:

Output = 0 or 1

Hypothesis => Z = Wx + B

hҩ(x) = Sigmoid(z)

There are two conditions:

Z = ∞ (infinity)

and

Y(predict) = 1

If Z = -∞

Y(predict) => 0

 
Before we implement any algorithm, we have to prepare data for it. Here are some data preparation methods for logistic regression.

 
Methodology

1. Data preparation
2. Binary output variable
3. Remove Noise
4. Gaussian distribution
5. Remove co-related Inputs

 
Examples of Usage

1. Credit Scoring
2. Medicine
3. Text Editing
4. Gaming

 
Advantages

Logistic regression is one of the most efficient techniques for solving classification problems. Some of the advantages of using logistic regression:

1. Logistic Regression is easy to implement, interpret and very efficient to train. It is very fast at classifying unknown records.
2. It performs well when the dataset is linearly separable.
3. It can interpret model coefficients as indicators of feature importance.

 
Disadvantages

1. It constructs linear boundaries; logistic regression needs that independent variable are linearly related to the odds.
2. The major limitation of logistic regression is the assumption of linearity between the dependent variable and the independent variable.
3. More powerful and compact algorithms such as neural networks can easily outperform this algorithm.

Conclusion

 
Logistic regression is one of the traditional machine learning methods. It forms a foundational set of ML approaches alongside algorithms such as linear regression, k-suggest clustering, major component analysis, and a few others. Neural networks have been developed leveraging logistic regression. You can efficiently use logistic regression even if you are not an ML specialist, not the case with many other algorithms. Conversely, it is not possible to become an ML master without a solif understanding of logistic regression.

 
 
Arvind Thorat is a Data Science Intern at NPPD.