Machine Learning from Scratch: Decision Trees
A simple explanation and implementation of DTs ID3 algorithm in Python

Image from Pexel
Decision trees are one of the simplest non-linear supervised algorithms in the machine learning world. As the name suggests they are used for making decisions in ML terms we call it classification (although they can be used for regression as well).
The decision trees have a unidirectional tree structure i.e. at every node the algorithm makes a decision to split into child nodes based on certain stopping criteria. Most commonly DTs use entropy, information gain, Gini index, etc.
There are a few known algorithms in DTs such as ID3, C4.5, CART, C5.0, CHAID, QUEST, CRUISE. In this article, we would discuss the simplest and most ancient one: ID3.
ID3, or Iternative Dichotomizer, was the first of three Decision Tree implementations developed by Ross Quinlan.
The algorithm builds a tree in a top-down fashion, starting from a set of rows/objects and a specification of features. At each node of the tree, one feature is tested based on minimizing entropy or maximizing information gain to split the object set. This process is continued until the set in a given node is homogeneous (i.e. node contains objects of the same category). The algorithm uses a greedy search. It selects a test using the information gain criterion, and then never explores the possibility of alternate choices.
Cons:
- The model may be over-fitted.
- Only works on categorical features
- Does not handle missing values
- Low speed
- Doesn’t support pruning
- Doesn’t support boosting
So many disadvantages of one algorithm, why are we even discussing this?
Answer: it’s simple and is great to develop the intuition for tree algorithms.
Let’s Understand with an Example
One of the most popular nursery rhyme where rain decides whether Johny/Arthur would play outside is our sample today. The only change is that not just rain but any bad weather impacts the child’s play and we would use a DT to predict his presence outside.

Source: Wikipedia
The data looks like this:
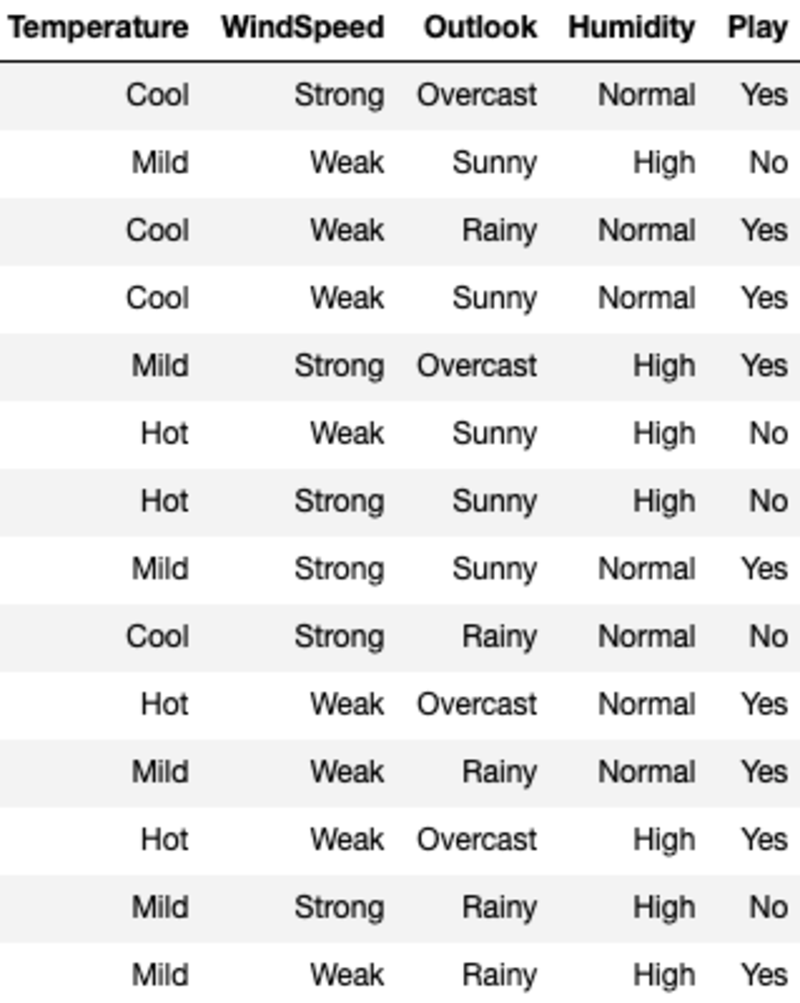
‘Temperature’, ‘WindSpeed’, ‘Outlook’, and ‘Humidity’ are the features, and ‘Play’ is the target variable. Only categorical data and no missing values mean we can use ID3.
Let’s go through the splitting criteria before jumping onto the algorithm itself. For simplicity, we will discuss each criterion only for the binary classification case.
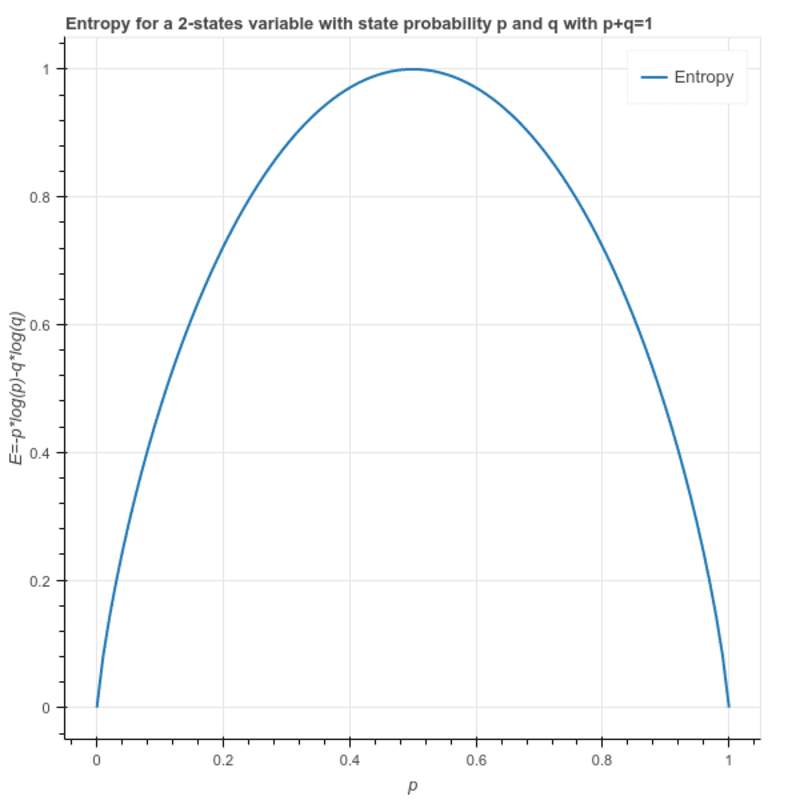
Entropy: This is used to calculate the heterogeneity of a sample and its value lies between 0 and 1. If the sample is homogeneous the entropy is 0 and if the sample has the same proportion of all the classes it has an entropy of 1.
S = -(p * log₂p + q * log₂q)
Where p and q are respective proportion of the 2 classes in the sample.
This can also be written as: S = -(p * log₂p + (1-p)* log₂(1-p))
Information Gain: It is the difference in entropy of a node and the average entropy for all the values of a child node. The feature which gives maximum Information Gain is chosen for the split.
Let’s Understand this with our Example
The entropy of root node: (9 — Yes and 5 — No)
S = -(9/14)*log(9/14) — (5/14) * log(5/14) = 0.94
There are 4 possible ways to split the root node. (‘Temperature’, ‘WindSpeed’, ‘Outlook’, and ‘Humidity’). Thus we compute the weighted average entropy of the child node if we choose any one of the above:
I(Temperature) = Hot*E(Temperature=Hot) + Mild*E(Temperature=Mild) + Cool*E(Temperature=Cool)
Where Hot, Mild, and Cool represent the proportion of the 3 values in the data.
I(Temperature) = (4/14)*1 + (6/14)*0.918 + (4/14)*0.811 = 0.911
Here Entropy for each value is computed by filtering the sample using the value of the feature and then using the formula for entropy. For example, E(Temperature=Hot) is computed by filtering the original sample where the Temperature is Hot (in this case we have an equal number of Yes and No which means Entropy equals 1).
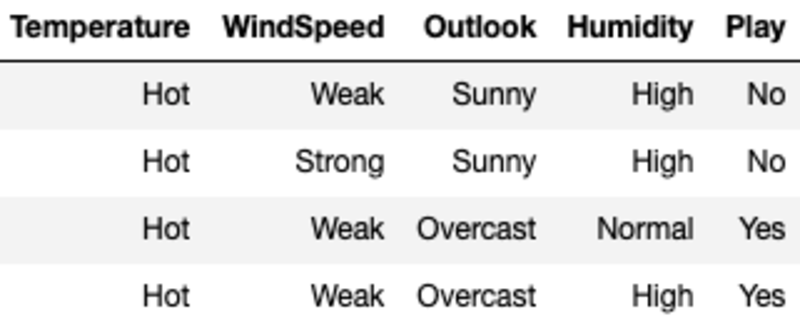
We compute the Information Gain of splitting on Temperature by subtracting the Average Entropy for Temperature from the root nodes Entropy.
G(Temperature) = S — I(Temperature) = 0.94–0.911 = 0.029
Likewise, we compute the Gain from all the four features and choose the 1 with maximum Gain.
G(WindSpeed) = S — I(WindSpeed) = 0.94–0.892 =0.048
G(Outlook) = S — I(Outlook) = 0.94–0.693 =0.247
G(Humidity) = S — I(Humidity) = 0.94–0.788 =0.152
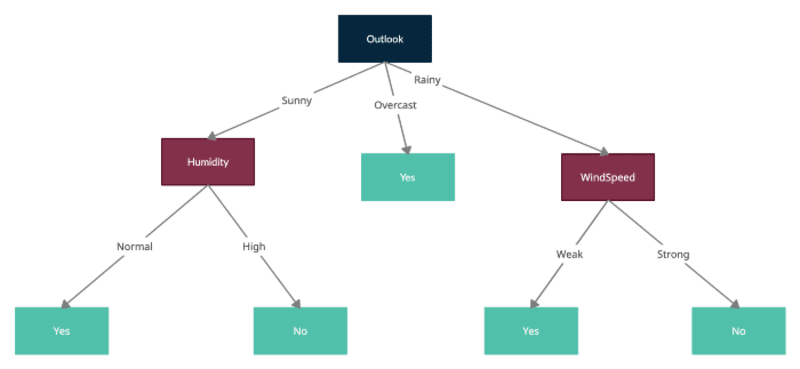
Outlook has the maximum Information Gain, thus we would split the root node on Outlook and each for the child nodes represents the sample filtered by one of the values of Outlook i.e. Sunny, Overcast, and Rainy.
Now we would repeat the same process by treating the new nodes formed as root nodes with filtered samples and compute entropies for each and testing the splits by computing Average Entropy for each further split and subtracting that from the current node Entropy to get the Information Gain. Please note that ID3 doesn’t allow using already used feature for splitting child nodes. Thus each feature can only be used once in a tree for the split.
Here is the final tree formed by all the splits:
Simple implementation with Python code can be found here
Conclusion
I tried my best to explain the ID3 working but I know you might have questions. Please let me know in the comments and I would be happy to take them all.
Thanks for reading!
Ankit Malik is building scalable AI/ML solutions across multiple domains like Marketing, Supply Chain, Retail, Advertising, and Process Automation. He has worked on both ends of the spectrum from leading data science projects in Fortune 500 companies to being the founding member of a data science incubator in multiple start-ups. He has pioneered various innovative products and services and is a believer in servant leadership.
Original. Reposted with permission.
