 PyTorch Tensor Basics
PyTorch Tensor Basics
This is an introduction to PyTorch's Tensor class, which is reasonably analogous to Numpy's ndarray, and which forms the basis for building neural networks in PyTorch.
Now that we know what a tensor is, and saw how Numpy's ndarray can be used to represent them, let's switch gears and see how they are represented in PyTorch.
PyTorch has made an impressive dent on the machine learning scene since Facebook open-sourced it in early 2017. It may not have the widespread adoption that TensorFlow has -- which was initially released well over a year prior, enjoys the backing of Google, and had the luxury of establishing itself as the gold standard as a new wave of neural networking tools was being ushered in -- but the attention that PyTorch receives in the research community especially is quite real. Much of this attention comes both from its relationship to Torch proper, and its dynamic computation graph.
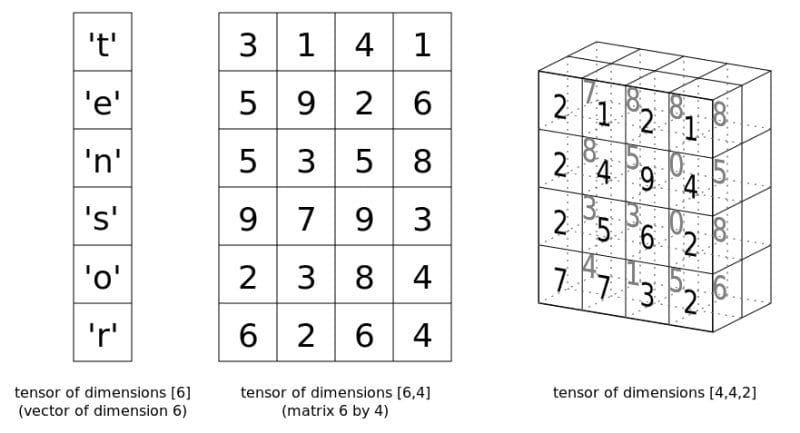
Image source
Tensor class, which is reasonably analogous to Numpy's ndarray.
Tensor (Very) Basics
So let's take a look at some of PyTorch's tensor basics, starting with creating a tensor (using the Tensor class):
import torch # Create a Torch tensor t = torch.Tensor([[1, 2, 3], [4, 5, 6]]) t
tensor([[ 1., 2., 3.],
[ 4., 5., 6.]])
You can transpose a tensor in one of 2 ways:
# Transpose t.t() # Transpose (via permute) t.permute(-1,0)
Both result in the following output:
tensor([[ 1., 4.],
[ 2., 5.],
[ 3., 6.]])
Note that neither result in a change to the original.
Reshape a tensor with view:
# Reshape via view t.view(3,2)
tensor([[ 1., 2.],
[ 3., 4.],
[ 5., 6.]])
And another example:
# View again... t.view(6,1)
tensor([[ 1.],
[ 2.],
[ 3.],
[ 4.],
[ 5.],
[ 6.]])
It should be obvious that mathematical conventions which are followed by Numpy carry over to PyTorch Tensors (specifically I'm referring to row and column notation).
Create a tensor and fill it with zeros (you can accomplish something similar with ones()):
# Create tensor of zeros t = torch.zeros(3, 3) t
tensor([[ 0., 0., 0.],
[ 0., 0., 0.],
[ 0., 0., 0.]])
Create a tensor with randoms pulled from the normal distribution:
# Create tensor from normal distribution randoms t = torch.randn(3, 3) t
tensor([[ 1.0274, -1.3727, -0.2196],
[-0.7258, -2.1236, -0.8512],
[ 0.0392, 1.2392, 0.5460]])
Shape, dimensions, and datatype of a tensor object:
# Some tensor info print('Tensor shape:', t.shape) # t.size() gives the same print('Number of dimensions:', t.dim()) print('Tensor type:', t.type()) # there are other types
Tensor shape: torch.Size([3, 3]) Number of dimensions: 2 Tensor type: torch.FloatTensor
It should also be obvious that, beyond mathematical concepts, a number of programmatic and instantiation similarities between ndarray and Tensor implementations exist.
You can slice PyTorch tensors the same way you slice ndarrays, which should be familiar to anyone who uses other Python structures:
# Slicing t = torch.Tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # Every row, only the last column print(t[:, -1]) # First 2 rows, all columns print(t[:2, :]) # Lower right most corner print(t[-1:, -1:])
tensor([ 3., 6., 9.])
tensor([[ 1., 2., 3.],
[ 4., 5., 6.]])
tensor([[ 9.]])
PyTorch Tensor To and From Numpy ndarray
You can easily create a tensors from an ndarray and vice versa. These operations are fast, since the data of both structures will share the same memory space, and so no copying is involved. This is obviously an efficient approach.
# Numpy ndarray <--> PyTorch tensor import numpy as np # ndarray to tensor a = np.random.randn(3, 5) t = torch.from_numpy(a) print(a) print(t) print(type(a)) print(type(t))
[[-0.52192738 -1.11579634 1.26925835 0.10449378 -1.02894372]
[-0.78707263 -0.05350072 -0.65815075 0.18810677 -0.52795765]
[-0.41677548 0.82031861 -2.46699201 0.60320375 -1.69778546]]
tensor([[-0.5219, -1.1158, 1.2693, 0.1045, -1.0289],
[-0.7871, -0.0535, -0.6582, 0.1881, -0.5280],
[-0.4168, 0.8203, -2.4670, 0.6032, -1.6978]], dtype=torch.float64)
<class 'numpy.ndarray'>
<class 'torch.Tensor'>
# tensor to ndarray t = torch.randn(3, 5) a = t.numpy() print(t) print(a) print(type(t)) print(type(a))
tensor([[-0.1746, -2.4118, 0.4688, -0.0517, -0.2706],
[-0.8402, -0.3289, 0.4170, 1.9131, -0.8601],
[-0.6688, -0.2069, -0.8106, 0.8582, -0.0450]])
[[-0.17455131 -2.4117854 0.4688457 -0.05168453 -0.2706456 ]
[-0.8402392 -0.3289494 0.41703534 1.9130518 -0.86014426]
[-0.6688193 -0.20693372 -0.8105542 0.8581988 -0.04502954]]
<class 'torch.Tensor'>
<class 'numpy.ndarray'>
Basic Tensor Operations
Here are a few tensor operations, which you can compare with Numpy implementations for fun. First up is the cross product:
# Compute cross product t1 = torch.randn(4, 3) t2 = torch.randn(4, 3) t1.cross(t2)
tensor([[ 2.6594, -0.5765, 1.4313],
[ 0.4710, -0.3725, 2.1783],
[-0.9134, 1.6253, 0.7398],
[-0.4959, -0.4198, 1.1338]])
Next is the matrix product:
# Compute matrix product t = (torch.Tensor([[2, 4], [5, 10]]).mm(torch.Tensor([[10], [20]]))) t
tensor([[ 100.],
[ 250.]])
And finally, elementwise multiplication:
# Elementwise multiplication t = torch.Tensor([[1, 2], [3, 4]]) t.mul(t)
tensor([[ 1., 4.],
[ 9., 16.]])
A Word About GPUs
PyTorch tensors have inherent GPU support. Specifying to use the GPU memory and CUDA cores for storing and performing tensor calculations is easy; the cuda package can help determine whether GPUs are available, and the package's cuda() method assigns a tensor to the GPU.
# Is CUDA GPU available? torch.cuda.is_available() # How many CUDA devices? torch.cuda.is_available() # Move to GPU t.cuda()
Related:

 PyTorch Tensor Basics
PyTorch Tensor Basics