Research Guide: Advanced Loss Functions for Machine Learning Models
This guide explores research centered on a variety of advanced loss functions for machine learning models.
In addition to good training data and the right model architecture, loss functions are one of the most important parts of training an accurate machine learning model. For this post, I’d love to give developers an overview of some of the more advanced loss functions and how they can be used to improve the accuracy of models—or solve entirely new tasks.
For example, semantic segmentation models typically use a simple cross-categorical entropy loss function during training, but if we want to segment objects with many fine details like hair, adding a gradient loss function to the model can vastly improve results.
This is just one example—the following guide explores research centered on a variety of advanced loss functions for machine learning models.
Robust Bi-Tempered Logistic Loss Based on Bregman Divergences
Logistic loss functions don’t perform very well during training when the data in question is very noisy. Such noise can be caused by outliers and mislabeled data. In this paper, Google Brain authors aim to solve the shortcomings of the logistic loss function by replacing the logarithm and exponential functions with their corresponding “tempered” versions.
Bi-Tempered Logistic Loss for Training Neural Nets with Noisy Data
The quality of models produced by machine learning (ML) algorithms directly depends on the quality of the training...
The authors introduce a temperature into the exponential function and replace the softmax output layer of neural nets with a high-temperature generalization. The algorithm used in the log loss is replaced by a low-temperature logarithm. The two temperatures are tuned to create loss functions that are nonconvex.
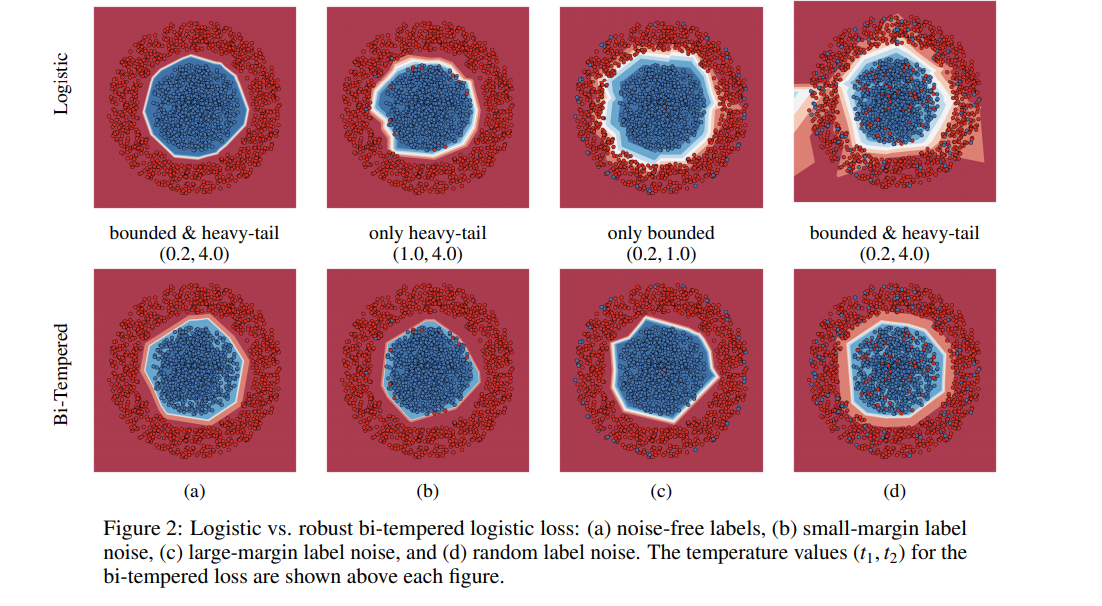
The last neural net layer is replaced with the bi-temperature generalization of the logistic loss. This makes the training process more robust to noise. The method proposed in this paper is based on Bregman divergences. Its performance can be visualized in the figure below.
For experimentation, the authors added synthetic noise to MNIST and CIFAR-100 datasets. The results obtained with their bi-temperature loss function was then compared to the vanilla logistic loss function. The bi-temperature loss obtains an accuracy of 98.56% on MNIST and 62.5% ON CIFAR-100. The figure below shows the performance in detail.
Machine learning models are moving closer and closer to edge devices. Fritz AI is here to help with this transition. Explore our suite of developer tools that makes it easy to teach devices to see, hear, sense, and think.
GANs Loss Functions
Discriminator loss aims at maximizing the probability given to real and fake images. Minimax loss is used in the paper that introduced GANs. This is a strategy aimed at reducing the worst-case-scenario possible loss. It’s simply minimizing the maximum loss. This loss is also used in two-player games to reduce the maximum loss for a layer.
Are GANs Created Equal? A Large-Scale Study
Generative adversarial networks (GAN) are a powerful subclass of generative models. Despite a very rich research...
In the case of GANs, the two players are the generator and discriminator. This involves the minimization of the generator’s loss and maximization of the discriminator’s loss. Modification of the discriminator loss forms the non-saturating GAN loss, whose aim is to tackle the saturation problem. This involves the generator maximizing the log of the discriminator probabilities. It is done for the generated images.
Least squares GAN loss was developed to counter the challenges of binary cross-entropy loss that resulted in the generated images being very different from the real images. This loss function is adopted for the discriminator. As a result of this, GANs using this loss function are able to generate higher quality images than regular GANs. A comparison of the two is shown in the next figure.
NIPS 2016 Tutorial: Generative Adversarial Networks
This report summarizes the tutorial presented by the author at NIPS 2016 on generative adversarial networks (GANs). The...
The Wasserstein loss function is dependent on the modification of the GAN architecture, where the discriminator doesn’t perform instance classification. Instead, the discriminator outputs a number for each instance. It attempts to make the number bigger for real instances than for fake ones.
In this loss function, the discriminator attempts to maximize the difference between the output on real instances and the output on fake instances. The generator, on the other hand, attempts to maximize the discriminator’s output for its fake instances.
Wasserstein GAN
We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we...
Here’s an image showing the performance of the GANs using this loss.
Focal Loss for Dense Object Detection
This paper proposes an improvement to the standard cross-entropy criterion by reshaping it such that it down-weights the loss assigned to the well-classified examples — focal loss. This loss function is aimed at solving the class imbalance problem.
Focal loss aims at training on a sparse set of hard examples and prevents easy negatives from trouncing the detector at training. For testing, the authors develop RetinaNet — a simple dense detector.
Focal Loss for Dense Object Detection
The highest accuracy object detectors to date are based on a two-stage approach popularized by R-CNN, where a...
In this loss function, the cross-entropy loss is scaled with the scaling factors decaying at zero as the confidence in the correct classes increases. The scaling factor automatically down weights the contribution of easy examples at training time and focuses on the hard ones.
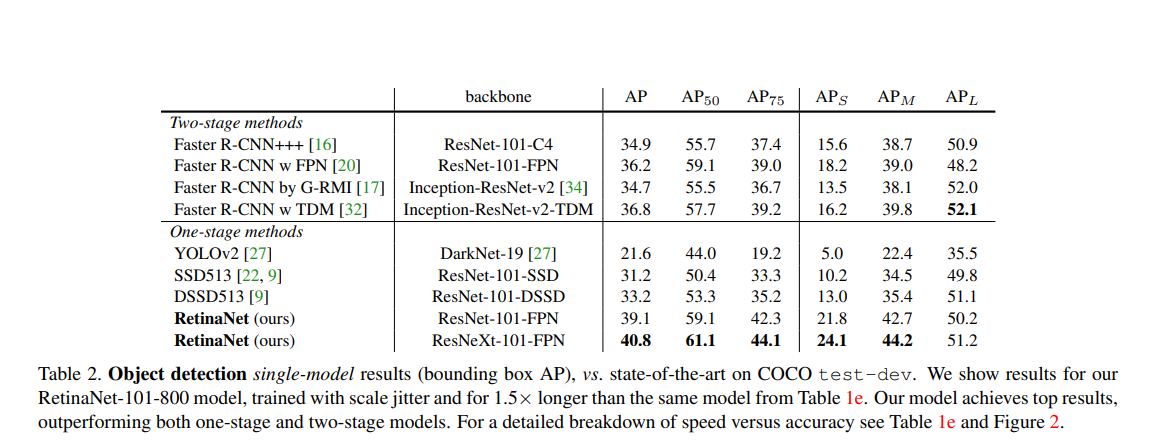
Here are the results obtained by the focal loss function on RetinaNet.
Intersection over Union (IoU)-balanced Loss Functions for Single-stage Object Detection
Loss functions adopted by single-stage detectors perform sub-optimally in localization. This paper proposes an IoU-based loss function that consists of IoU-balanced classification and IoU-balanced localization loss.
IoU-balanced Loss Functions for Single-stage Object Detection
Single-stage detectors are efficient. However, we find that the loss functions adopted by single-stage detectors are...
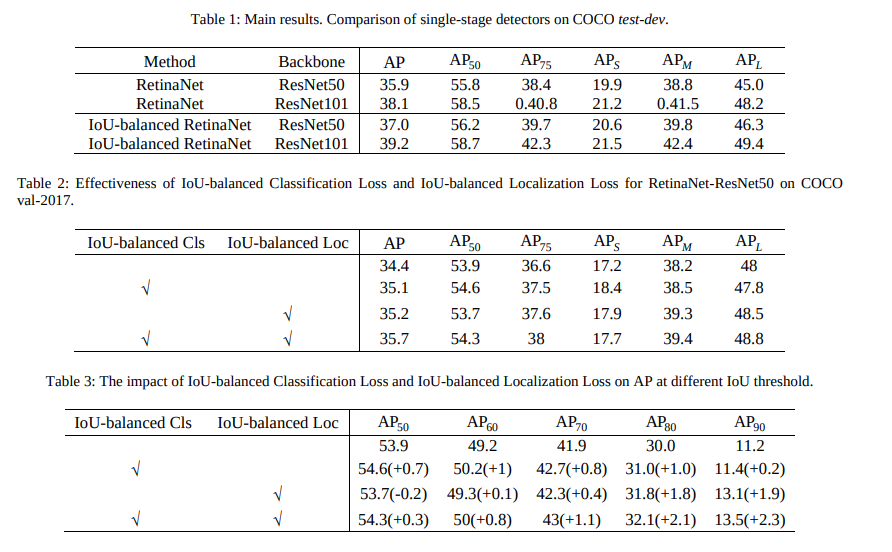
The IoU-balanced classification loss focuses on positive scenarios with high IoU can increase the correlation between classification and the task of localization. The loss aims at decreasing the gradient of the examples with low IoU and increasing the gradient of examples with high IoU. This increases the localization accuracy of models.
The loss’s performance on the COCO dataset is shown below.
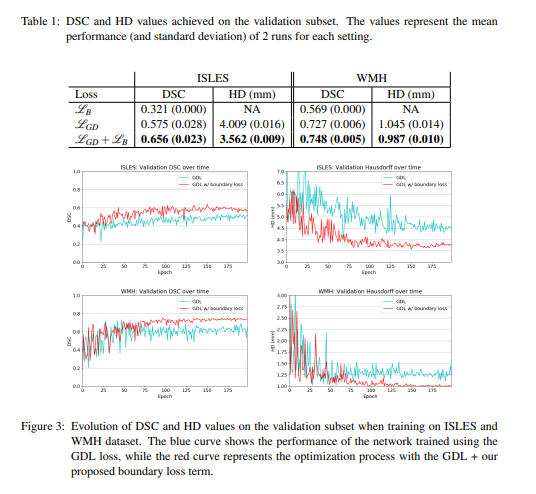
Boundary loss for highly unbalanced segmentation
This paper proposes a boundary loss for highly unbalanced segmentations. The loss takes the form of a distance metric on the space of contours and not regions. This is done to tackle the challenges of regional losses for highly unbalanced segmentation problems. The loss is inspired by discrete optimization techniques for computing gradient flows of curve evolution.
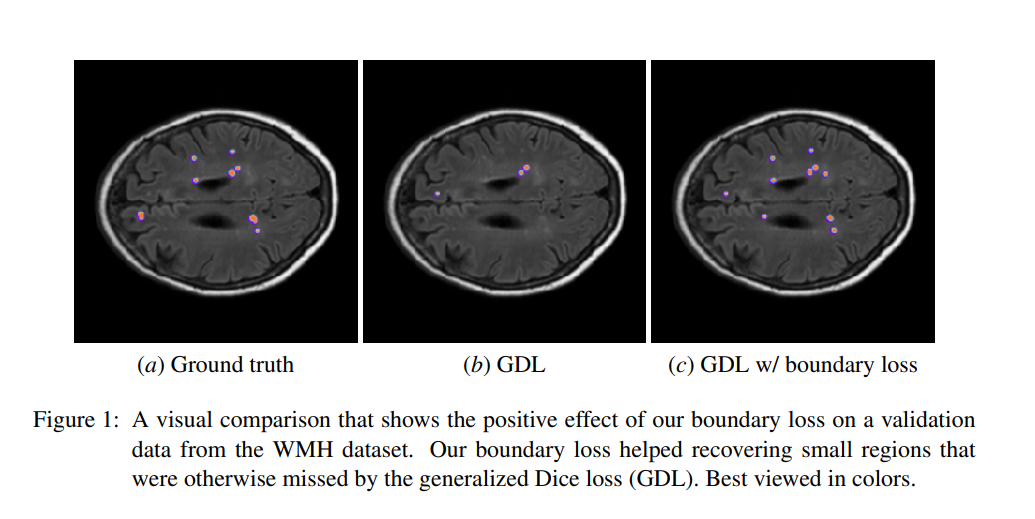
The boundary loss uses integrals over the boundary between regions as opposed to using unbalanced integrals over the regions. An integral approach for computing boundary variations is used. The authors express a non-symmetric L2 distance on the space of shapes as a regional integral. This avoids local differential computations involving contour points. This then yields a boundary loss that’s expressed as the sum of the regional softmax probability outputs of the network. The loss is easily combined with regional losses and incorporated in existing deep network architectures.
The boundary loss was tested on the Ischemic Stroke Lesion (ISLES) and the White Matter Hyperintensities (WMH) benchmark datasets.
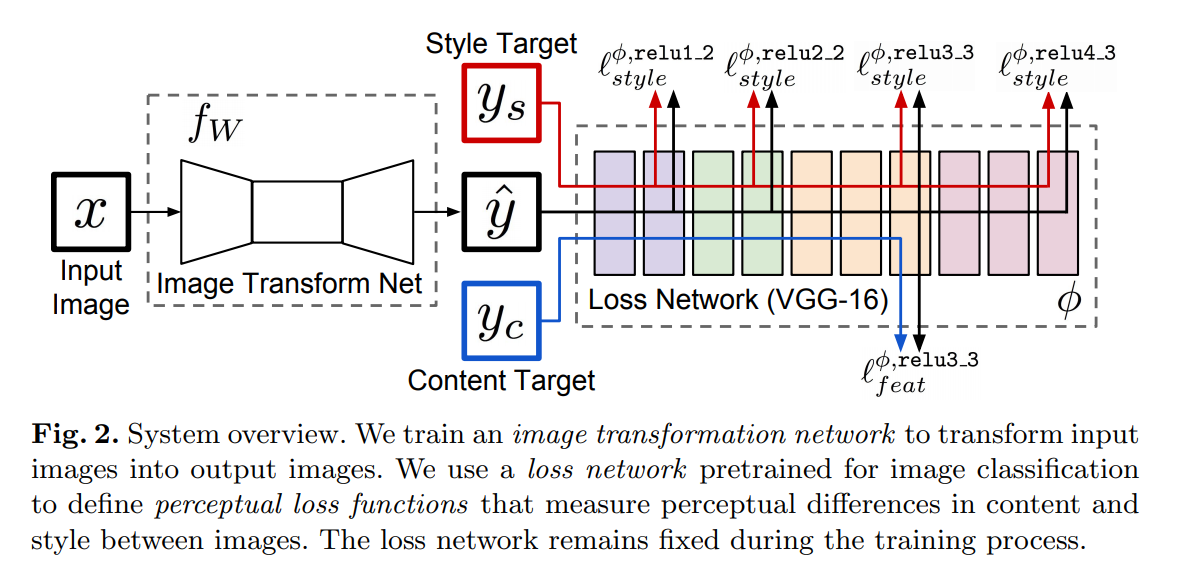
Perceptual Loss Function
This loss function is used when images that look similar are being compared. The loss function is primarily used for training feedforward neural networks for tasks image transformation tasks.
Perceptual Losses for Real-Time Style Transfer and Super-Resolution
We consider image transformation problems, where an input image is transformed into an output image. Recent methods for...
The perceptual loss function works by adding the squared errors in the middle of all pixels and calculating the mean.
In style transfer, perceptual loss enables deep learning models to reconstruct finer details better than other loss functions. At training time, perceptual losses measure image similarities better than per-pixel loss functions. They also enable the transfer of semantic knowledge from the loss network to the transformation network.
Conclusion
We should now be up to speed on some of the most common — and a couple of very recent — advanced loss functions.
The papers/abstracts mentioned and linked to above also contain links to their code implementations. We’d be happy to see the results you obtain after testing them.
Bio: Derrick Mwiti is a data analyst, a writer, and a mentor. He is driven by delivering great results in every task, and is a mentor at Lapid Leaders Africa.
Original. Reposted with permission.
Related:
- Research Guide for Neural Architecture Search
- Research Guide for Transformers
- Research Guide for Video Frame Interpolation with Deep Learning