Classify A Rare Event Using 5 Machine Learning Algorithms
Which algorithm works best for unbalanced data? Are there any tradeoffs?
By Leihua Ye, UC Santa Barbara
Machine Learning is the crown of Data Science;
Supervised Learning is the crown jewel of Machine Learning.
Background
A couple years ago, Harvard Business Review released an article with the following title “Data Scientist: The Sexiest Job of the 21st Century.” Ever since its release, Data Science or Statistics Departments become widely pursued by college students and, and Data Scientists (Nerds), for the first time, is referred to as being sexy.
For some industries, Data Scientists have reshaped the corporation structure and reallocated a lot of decision-makings to the “front-line” workers. Being able to generate useful business insights from data has never been so easy.
According to Andrew Ng (Machine Learning Yearning, p.9),
Supervised Learning algorithms contribute the majority value to the industry.
There is no doubt why SL generates so much business value. Banks use it to detect credit card fraud, traders make purchase decisions based on what models tell them to, and factory filter through the production line for defective units (this is an area where AI and ML can help traditional companies, according to Andrew Ng).
These business scenarios share two common features:
- Binary Results: fraud VS not fraud, to buy VS not to buy, and defective VS not defective.
- Imbalanced Data Distribution: one majority group VS one minority group.
As Andrew Ng points out recently, small data, robustness, and human factor are three obstacles to successful AI projects. To a certain degree, our rare event question with one minority group is also a small data question: the ML algorithm learns more from the majority group and may easily misclassify the small data group.
Here are the million-dollar questions:
For these rare events, which ML method performs better?
What metrics?
Tradeoffs?
In this post, we try to answer these questions by applying 5 ML methods to a real-life dataset with comprehensive R implementations.
For the full description and the original dataset, please check the original dataset; For the complete R code, please check my Github.
Business Question
A bank in Portugal carries out a marketing strategy of a new banking service (a term deposit) and wants to know which types of clients have subscribed to the service. So, the bank can adjust its marketing strategy and target specific groups of populations in the future. Data Scientists have teamed up with the sells and marketing teams to come up with statistical solutions to identify future subscribers.
R Implementations
Here comes the pipeline of model selection and R implementations.
1. Importation, Data Cleaning, and Exploratory Data Analysis
Let’s load and clean the raw dataset.
####load the dataset banking=read.csv(“bank-additional-full.csv”,sep =”;”,header=T)##check for missing data and make sure no missing data banking[!complete.cases(banking),]#re-code qualitative (factor) variables into numeric banking$job= recode(banking$job, “‘admin.’=1;’blue-collar’=2;’entrepreneur’=3;’housemaid’=4;’management’=5;’retired’=6;’self-employed’=7;’services’=8;’student’=9;’technician’=10;’unemployed’=11;’unknown’=12”)#recode variable again banking$marital = recode(banking$marital, “‘divorced’=1;’married’=2;’single’=3;’unknown’=4”)banking$education = recode(banking$education, “‘basic.4y’=1;’basic.6y’=2;’basic.9y’=3;’high.school’=4;’illiterate’=5;’professional.course’=6;’university.degree’=7;’unknown’=8”)banking$default = recode(banking$default, “‘no’=1;’yes’=2;’unknown’=3”)banking$housing = recode(banking$housing, “‘no’=1;’yes’=2;’unknown’=3”)banking$loan = recode(banking$loan, “‘no’=1;’yes’=2;’unknown’=3”) banking$contact = recode(banking$loan, “‘cellular’=1;’telephone’=2;”)banking$month = recode(banking$month, “‘mar’=1;’apr’=2;’may’=3;’jun’=4;’jul’=5;’aug’=6;’sep’=7;’oct’=8;’nov’=9;’dec’=10”)banking$day_of_week = recode(banking$day_of_week, “‘mon’=1;’tue’=2;’wed’=3;’thu’=4;’fri’=5;”)banking$poutcome = recode(banking$poutcome, “‘failure’=1;’nonexistent’=2;’success’=3;”)#remove variable “pdays”, b/c it has no variation banking$pdays=NULL #remove variable “pdays”, b/c itis collinear with the DV banking$duration=NULL
It appears to be tedious to clean the raw data as we have to recode missing variables and transform qualitative into quantitative variables. It takes even more time to clean the data in the real world. There is a saying “data scientists spend 80% of their time cleaning data and 20% building a model.”
Next, let’s explore the distribution of our outcome variables.
#EDA of the DV plot(banking$y,main="Plot 1: Distribution of Dependent Variable")

As can be seen, the dependent variables (service subscription) are not equally distributed, with more “No”s than “Yes”s. The unbalanced distribution should flash some warning signs because data distribution affects the final statistical model. It can easily misclassify the minority case using a model developed out of a majority case.
2. Data Split
Next, let’s split the dataset into two parts: training and test sets. As a rule of thumb, we stick to the 80–20 division: 80% as the training set and 20% as the test test. For Time Series data, we train models based on 90% of the data and leave the rest 10% as the test dataset.
#split the dataset into training and test sets randomly set.seed(1)#set seed so as to generate the same value each time we run the code#create an index to split the data: 80% training and 20% test index = round(nrow(banking)*0.2,digits=0)#sample randomly throughout the dataset and keep the total number equal to the value of index test.indices = sample(1:nrow(banking), index)#80% training set banking.train=banking[-test.indices,] #20% test set banking.test=banking[test.indices,] #Select the training set except the DV YTrain = banking.train$y XTrain = banking.train %>% select(-y)# Select the test set except the DV YTest = banking.test$y XTest = banking.test %>% select(-y)
Here, let’s create an empty tracking record.
records = matrix(NA, nrow=5, ncol=2) colnames(records) <- c(“train.error”,”test.error”) rownames(records) <- c(“Logistic”,”Tree”,”KNN”,”Random Forests”,”SVM”)
3. Train Models
In this section, we define a new function (calc_error_rate) and apply it to calculate training and test errors of each ML model.
calc_error_rate <- function(predicted.value, true.value)
{return(mean(true.value!=predicted.value))}
This function calculates the rate when the predicted label does not equal to the true value.
#1 Logistic Regression Model
For a brief introduction of logistic model, please check my other posts: Machine Learning 101and Machine Learning 102.
Let’s fit a logistic model including all other variables except the outcome variable. Since the outcome is binary, we set the model to binomial distribution (“family=binomial”).
glm.fit = glm(y ~ age+factor(job)+factor(marital)+factor(education)+factor(default)+factor(housing)+factor(loan)+factor(contact)+factor(month)+factor(day_of_week)+campaign+previous+factor(poutcome)+emp.var.rate+cons.price.idx+cons.conf.idx+euribor3m+nr.employed, data=banking.train, family=binomial)
The next step is to obtain the train error. We set the type to response since we are predicting the types of the outcome and adopt a majority rule: if the prior probability exceeding or equal to 0.5, we predict the outcome to be a yes; otherwise, a no.
prob.training = predict(glm.fit,type=”response”)banking.train_glm = banking.train %>% #select all rows of the train mutate(predicted.value=as.factor(ifelse(prob.training<=0.5, “no”, “yes”))) #create a new variable using mutate and set a majority rule using ifelse# get the training error logit_traing_error <- calc_error_rate(predicted.value=banking.train_glm$predicted.value, true.value=YTrain)# get the test error of the logistic model prob.test = predict(glm.fit,banking.test,type=”response”)banking.test_glm = banking.test %>% # select rows mutate(predicted.value2=as.factor(ifelse(prob.test<=0.5, “no”, “yes”))) # set ruleslogit_test_error <- calc_error_rate(predicted.value=banking.test_glm$predicted.value2, true.value=YTest)# write down the training and test errors of the logistic model records[1,] <- c(logit_traing_error,logit_test_error)#write into the first row
#2 Decision Tree
For DT, we follow cross-validation and identify the best nodes of split. For a quick intro to DT, please refer to a post (link) by Prashant Gupta.
# finding the best nodes # the total number of rows nobs = nrow(banking.train)#build a DT model; #please refer to this document (here) for constructing a DT model bank_tree = tree(y~., data= banking.train,na.action = na.pass, control = tree.control(nobs , mincut =2, minsize = 10, mindev = 1e-3))#cross validation to prune the tree set.seed(3) cv = cv.tree(bank_tree,FUN=prune.misclass, K=10) cv#identify the best cv best.size.cv = cv$size[which.min(cv$dev)] best.size.cv#best = 3bank_tree.pruned<-prune.misclass(bank_tree, best=3) summary(bank_tree.pruned)
The best size of cross-validation is 3.
# Training and test errors of bank_tree.pruned pred_train = predict(bank_tree.pruned, banking.train, type=”class”) pred_test = predict(bank_tree.pruned, banking.test, type=”class”)# training error DT_training_error <- calc_error_rate(predicted.value=pred_train, true.value=YTrain)# test error DT_test_error <- calc_error_rate(predicted.value=pred_test, true.value=YTest)# write down the errors records[2,] <- c(DT_training_error,DT_test_error)
#3 K-Nearest Neighbors
As a non-parametric method, KNN does not require any prior knowledge of the distribution. In simple words, KNN assigns a k number of nearest neighbors to the unit of interest.
For a quick start, please check my post on KNN: Beginner’s Guide to K-Nearest Neighbors in R: from Zero to Hero. For detailed explanations of Cross-Validation and the do.chunk function, please redirect to my post.
Using cross-validation, we find the minimal cross-validation error when k=20.
nfold = 10
set.seed(1)# cut() divides the range into several intervals
folds = seq.int(nrow(banking.train)) %>%
cut(breaks = nfold, labels=FALSE) %>%
sampledo.chunk <- function(chunkid, folddef, Xdat, Ydat, k){
train = (folddef!=chunkid)# training indexXtr = Xdat[train,] # training set by the indexYtr = Ydat[train] # true label in training setXvl = Xdat[!train,] # test setYvl = Ydat[!train] # true label in test setpredYtr = knn(train = Xtr, test = Xtr, cl = Ytr, k = k) # predict training labelspredYvl = knn(train = Xtr, test = Xvl, cl = Ytr, k = k) # predict test labelsdata.frame(fold =chunkid, # k folds
train.error = calc_error_rate(predYtr, Ytr),#training error per fold
val.error = calc_error_rate(predYvl, Yvl)) # test error per fold
}# set error.folds to save validation errors
error.folds=NULL# create a sequence of data with an interval of 10
kvec = c(1, seq(10, 50, length.out=5))set.seed(1)for (j in kvec){
tmp = ldply(1:nfold, do.chunk, # apply do.function to each fold
folddef=folds, Xdat=XTrain, Ydat=YTrain, k=j) # required arguments
tmp$neighbors = j # track each value of neighbors
error.folds = rbind(error.folds, tmp) # combine the results
}#melt() in the package reshape2 melts wide-format data into long-format data
errors = melt(error.folds, id.vars=c(“fold”,”neighbors”), value.name= “error”)
Then, let’s find the best k number that minimizes validation error.
val.error.means = errors %>% filter(variable== “val.error” ) %>% group_by(neighbors, variable) %>% summarise_each(funs(mean), error) %>% ungroup() %>% filter(error==min(error))#the best number of neighbors =20 numneighbor = max(val.error.means$neighbors) numneighbor## [20]
Following the same step, we find the training and test errors.
#training error set.seed(20) pred.YTtrain = knn(train=XTrain, test=XTrain, cl=YTrain, k=20) knn_traing_error <- calc_error_rate(predicted.value=pred.YTtrain, true.value=YTrain)#test error =0.095set.seed(20) pred.YTest = knn(train=XTrain, test=XTest, cl=YTrain, k=20) knn_test_error <- calc_error_rate(predicted.value=pred.YTest, true.value=YTest)records[3,] <- c(knn_traing_error,knn_test_error)
#4 Random Forests
We follow standard steps of constructing a Random Forests model. A quick intro to RF (link) by Tony Yiu.
# build a RF model with default settings set.seed(1) RF_banking_train = randomForest(y ~ ., data=banking.train, importance=TRUE)# predicting outcome classes using training and test sets pred_train_RF = predict(RF_banking_train, banking.train, type=”class”)pred_test_RF = predict(RF_banking_train, banking.test, type=”class”)# training error RF_training_error <- calc_error_rate(predicted.value=pred_train_RF, true.value=YTrain)# test error RF_test_error <- calc_error_rate(predicted.value=pred_test_RF, true.value=YTest)records[4,] <- c(RF_training_error,RF_test_error)
#5 Support Vector Machines
Similarly, we follow standard steps of constructing SVM. A good intro to the method, please refer to a post (Link) by Rohith Gandhi.
set.seed(1) tune.out=tune(svm, y ~., data=banking.train, kernel=”radial”,ranges=list(cost=c(0.1,1,10)))# find the best parameters summary(tune.out)$best.parameters# the best model best_model = tune.out$best.modelsvm_fit=svm(y~., data=banking.train,kernel=”radial”,gamma=0.05555556,cost=1,probability=TRUE)# using training/test sets to predict outcome classes svm_best_train = predict(svm_fit,banking.train,type=”class”) svm_best_test = predict(svm_fit,banking.test,type=”class”)# training error svm_training_error <- calc_error_rate(predicted.value=svm_best_train, true.value=YTrain)# test error svm_test_error <- calc_error_rate(predicted.value=svm_best_test, true.value=YTest)records[5,] <- c(svm_training_error,svm_test_error)
4. Model Metrics
We have constructed all ML models following model selection procedures and obtained their training and test errors. In this section, we are going to select the best model using some model metrics.
4.1 Train/Test Errors
Is it possible to find the best model using the train/test errors?
Now, let’s check the results.
records

Here, Random Forests have the minimal training error, though with a similar test error with the other methods. As you may notice, the training and test errors are very close, and it’s difficult to tell which one is clearly winning.
Besides, classification accuracy, either train error or test error, should not be the metrics for highly imbalanced dataset. This is so because the dataset is dominated by the majority cases, and even a random guess gives you 50–50 chance of getting it right (50% accuracy). Even worse, a highly accuracy model may severely penalize the minority case. For that reason, let’s check another metrics ROC Curve.
4.2 Receiver Operating Characteristic (ROC) Curve
ROC is a graphic representation showing how a classification model performs at all classification thresholds. We prefer a classifier that approaches to 1 quicker than others.
ROC Curve plots two parameters — True Positive Rate and False Positive Rate — at different thresholds in the same graph:
TPR (Recall) = TP/(TP+FN)
FPR = FP/(TN+FP)
To a large extent, ROC Curve does not only measure the level of classification accuracy but reaches a nice balance between TPR and FPR. This is quite desirable for rare events since we also want to reach a balance between the majority and minority cases.
# load the library library(ROCR)#creating a tracking record Area_Under_the_Curve = matrix(NA, nrow=5, ncol=1) colnames(Area_Under_the_Curve) <- c(“AUC”) rownames(Area_Under_the_Curve) <- c(“Logistic”,”Tree”,”KNN”,”Random Forests”,”SVM”)########### logistic regression ########### # ROC prob_test <- predict(glm.fit,banking.test,type=”response”) pred_logit<- prediction(prob_test,banking.test$y) performance_logit <- performance(pred_logit,measure = “tpr”, x.measure=”fpr”)########### Decision Tree ########### # ROC pred_DT<-predict(bank_tree.pruned, banking.test,type=”vector”) pred_DT <- prediction(pred_DT[,2],banking.test$y) performance_DT <- performance(pred_DT,measure = “tpr”,x.measure= “fpr”)########### KNN ########### # ROC knn_model = knn(train=XTrain, test=XTrain, cl=YTrain, k=20,prob=TRUE)prob <- attr(knn_model, “prob”) prob <- 2*ifelse(knn_model == “-1”, prob,1-prob) — 1 pred_knn <- prediction(prob, YTrain) performance_knn <- performance(pred_knn, “tpr”, “fpr”)########### Random Forests ########### # ROC pred_RF<-predict(RF_banking_train, banking.test,type=”prob”) pred_class_RF <- prediction(pred_RF[,2],banking.test$y) performance_RF <- performance(pred_class_RF,measure = “tpr”,x.measure= “fpr”)########### SVM ########### # ROC svm_fit_prob = predict(svm_fit,type=”prob”,newdata=banking.test,probability=TRUE) svm_fit_prob_ROCR = prediction(attr(svm_fit_prob,”probabilities”)[,2],banking.test$y==”yes”) performance_svm <- performance(svm_fit_prob_ROCR, “tpr”,”fpr”)
Let’s plot the ROC curves.
We put a abline to show the chance of random assignment. Our classifier should perform better than random guess, right?
#logit plot(performance_logit,col=2,lwd=2,main=”ROC Curves for These Five Classification Methods”)legend(0.6, 0.6, c(‘logistic’, ‘Decision Tree’, ‘KNN’,’Random Forests’,’SVM’), 2:6)#decision tree plot(performance_DT,col=3,lwd=2,add=TRUE)#knn plot(performance_knn,col=4,lwd=2,add=TRUE)#RF plot(performance_RF,col=5,lwd=2,add=TRUE)# SVM plot(performance_svm,col=6,lwd=2,add=TRUE)abline(0,1)
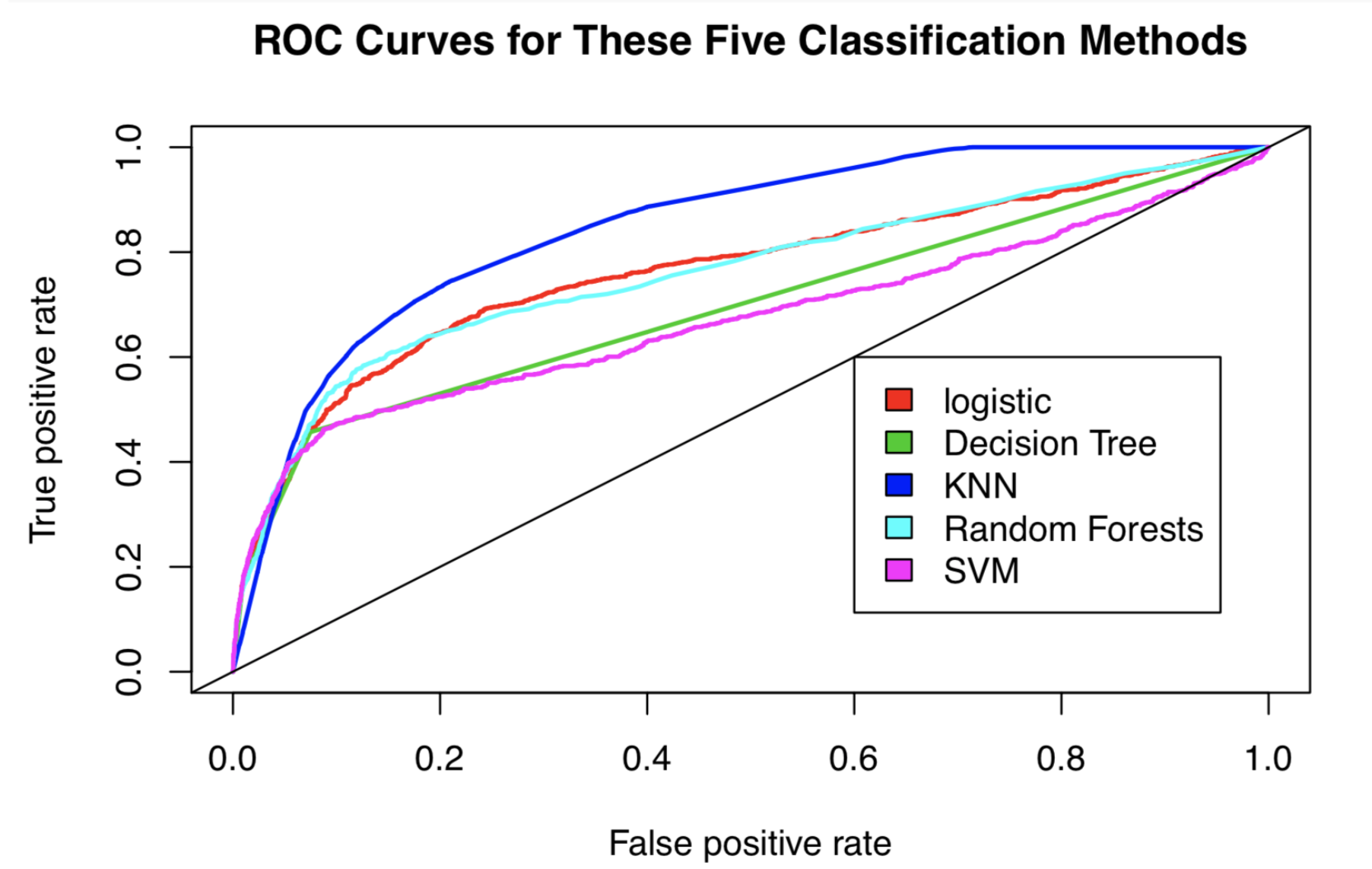
We have a winner here.
According to the ROC curve, KNN (the blue one) stands above all other methods.
4.3 Area Under the Curve (AUC)
As the name suggested, AUC is the area under the ROC curve. It is an arithmetic representation of the visual AUC curve. AUC provides an aggregated results of how classifiers perform across possible classifcation thresholds.
########### Logit ########### auc_logit = performance(pred_logit, “auc”)@y.values Area_Under_the_Curve[1,] <-c(as.numeric(auc_logit))########### Decision Tree ########### auc_dt = performance(pred_DT,”auc”)@y.values Area_Under_the_Curve[2,] <- c(as.numeric(auc_dt))########### KNN ########### auc_knn <- performance(pred_knn,”auc”)@y.values Area_Under_the_Curve[3,] <- c(as.numeric(auc_knn))########### Random Forests ########### auc_RF = performance(pred_class_RF,”auc”)@y.values Area_Under_the_Curve[4,] <- c(as.numeric(auc_RF))########### SVM ########### auc_svm<-performance(svm_fit_prob_ROCR,”auc”)@y.values[[1]] Area_Under_the_Curve[5,] <- c(as.numeric(auc_svm))
Let’s check the AUC values.
Area_Under_the_Curve

Also, KNN has the biggest AUC value (0.847).
Conclusion
In this post, we find KNN, a non-parametric classifier, performs better than its parametric counterparts. In terms of metrics, it’s more reasonable to choose ROC Curve over classification accuracy for rare events.
Enjoy reading this one?
Please find me at LinkedIn and Twitter.
Check out my other posts on Artificial Intelligence and Machine Learning.
Beginner’s Guide to K-Nearest Neighbors in R: from Zero to Hero
A pipeline of building a KNN model in R with various measurement metrics
Machine Learning 101: Predicting Drug Use Using Logistic Regression In R
Basics, link functions, and plots
Machine Learning 102: Logistic Regression With Polynomial Features
How to classify when there are nonlinear components
Bio: Leihua Ye (@leihua_ye)is a Ph.D. Candidate at the UC, Santa Barbara. He has 5+ years of research and professional experience in Quantitative UX Research, Experimentation & Causal Inference, Machine Learning, and Data Science.
Original. Reposted with permission.
Related:
- Beginner’s Guide to K-Nearest Neighbors in R: from Zero to Hero
- Classifying Heart Disease Using K-Nearest Neighbors
- How to Visualize Data in Python (and R)

