An Introduction to Markov Chains
Markov chains are often used to model systems that exhibit memoryless behavior, where the system's future behavior is not influenced by its past behavior.

Image from Unsplash
Introduction
Markov chains are a type of mathematical system that undergoes transitions from one state to another according to certain probabilistic rules. They were first introduced by Andrey Markov in 1906 as a way to model the behavior of random processes, and have since been applied to a wide range of fields, including physics, biology, economics, statistics, machine learning, and computer science.
Markov chains are named after Andrey Markov, a Russian mathematician who is credited with developing the theory of these systems in the early 20th century. Markov was interested in understanding the behavior of random processes, and he developed the theory of Markov chains as a way to model such processes.
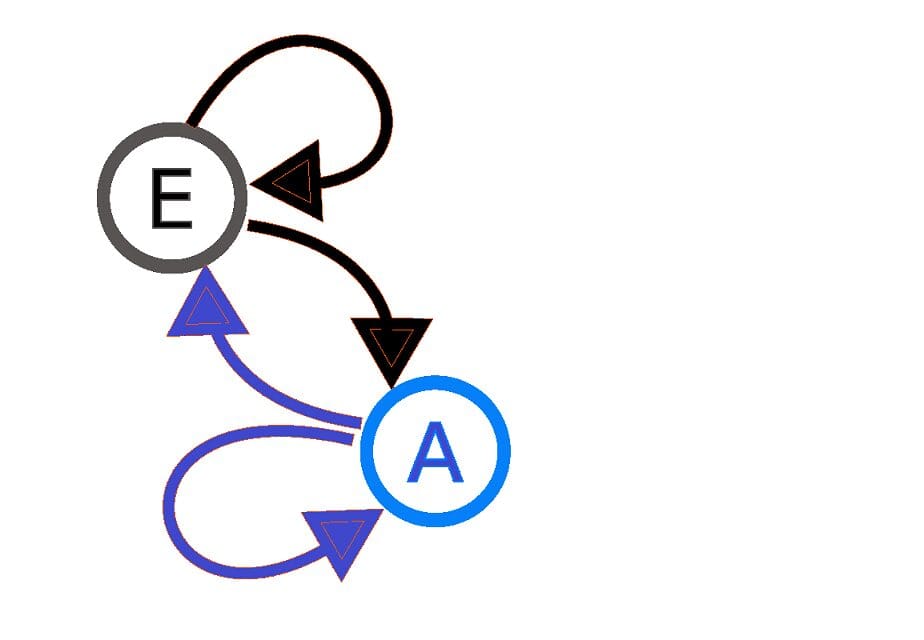
Fig 1. Visualization of a two-state Markov system: the arrows indicate the transitions between states.
Markov chains are often used to model systems that exhibit memoryless behavior, where the system's future behavior is not influenced by its past behavior.
A common application of Markov chains in data science is text prediction. It’s an area of NLP (Natural Language Processing) that is commonly used in the tech industry by companies like Google, LinkedIn, and Instagram. When you’re writing emails, Google predicts and suggests words or phrases to autocomplete your email. And when you receive messages on Instagram or LinkedIn, those apps suggest potential replies. These are the applications of a Markov chain we will explore. That said, the types of models these large-scale companies use in production for these features are more complicated.
In data science, Markov chains can also be used to model a wide range of phenomena, including the evolution of time series data, the movement of particles in a gas, the spread of diseases, and the behavior of financial markets.
Time Series Example
Here is an example of how a Markov chain might be used to model the evolution of a time series:
Suppose we have a time series of stock prices, and we want to use a Markov chain to model the evolution of the stock's price over time. We can define a set of states that the stock's price can take on (e.g. "increasing," "decreasing," and "stable"), and specify the probability of transitioning between these states. For example, we might define the transition probabilities as follows:
Increasing Decreasing Stable
Increasing 0.6 0.3 0.1
Decreasing 0.4 0.4 0.2
Stable 0.5 0.3 0.2
This matrix specifies the probability of transitioning from one state to another given the current state. For example, if the stock's price is currently increasing, there is a 60% chance that it will continue to increase, a 30% chance that it will decrease, and a 10% chance that it will remain stable.
Once we have defined the Markov chain and its transition probabilities, we can use it to predict the future evolution of the stock's price by simulating the transitions between states. At each time step, we would use the current state and the transition probabilities to determine the probability of transitioning to each possible next state.
Limitations
One limitation of Markov chains is that they are only applicable to systems that exhibit memoryless behavior. This means that the future behavior of the system is not influenced by its past behavior. If the system does exhibit memory, then a Markov chain may not be the most appropriate tool for modeling its behavior.
Another limitation of Markov chains is that they can only model systems that have a finite number of states. If the system can take on an infinite number of states, then a Markov chain may not be able to accurately model its behavior.
Markov chains can only model systems that exhibit stationary behavior, where the transition probabilities between states do not change over time. If the transition probabilities do change over time, then a more complex model may be required to accurately capture the behavior of the system.
Example in Python
Here is an example of how to implement a Markov chain in Python:
Modeling the stock price to predict whether it is increasing, decreasing, or stable.
import numpy as np
# Define the states of the Markov chain
states = ["increasing", "decreasing", "stable"]
# Define the transition probabilities
transition_probs = np.array([[0.6, 0.3, 0.1], [0.4, 0.4, 0.2], [0.5, 0.3, 0.2]])
# Set the initial state
current_state = "increasing"
# Set the number of time steps to simulate
num_steps = 10
# Simulate the Markov chain for the specified number of time steps
for i in range(num_steps):
# Get the probability of transitioning to each state
probs = transition_probs[states.index(current_state)]
# Sample a new state from the distribution
new_state = np.random.choice(states, p=probs)
# Update the current state
current_state = new_state
# Print the current state
print(f"Step {i+1}: {current_state}")
This code defines a simple Markov chain with three states ("increasing," "decreasing," and "stable") and specifies the transition probabilities between these states. It then simulates the Markov chain for 10 time steps, sampling a new state at each time step according to the transition probabilities and updating the current state accordingly. The output of this code will be a sequence of states representing the evolution of the system over time, as shown below:

Fig 2. Output from a three state Markov process, with initial state set as “increasing”.
If we set the current state to “decreasing” and run the code, we obtain the following output:

Fig 3. Output from a three state Markov process, with initial state set as “decreasing”.
Note that this is a very simplified example, and in practice, you may need to use more states and consider more complex transition probabilities in order to model the behavior of the system accurately. However, this illustrates the basic idea of how a Markov chain can be implemented in Python.
Markov chains can be applied to a wide range of problems, and they can be implemented in Python using a variety of tools and libraries, including 'numpy' and the scipy.stats library.
However, it is important to carefully consider the assumptions of Markov chains and whether they are suitable for a particular problem before using them to model a system. To conclude, Markov chains are a useful tool for data scientists and researchers to consider when analyzing and modeling systems that exhibit certain types of behavior.
Benjamin O. Tayo is a Physicist, Data Science Educator, and Writer, as well as the Owner of DataScienceHub. Previously, Benjamin was teaching Engineering and Physics at U. of Central Oklahoma, Grand Canyon U., and Pittsburgh State U.
