Custom Optimizer in TensorFlow
How to customize the optimizers to speed-up and improve the process of finding a (local) minimum of the loss function using TensorFlow.
By Benoit Descamps, BigData Republic.
Introduction
Neural Networks play a very important role when modeling unstructured data such as in Language or Image processing. The idea of such networks is to simulate the structure of the brain using nodes and edges with numerical weights processed by activation functions. The output of such networks mostly yield a prediction, such as a classification. This is achieved by optimizing on a given target using some optimisation loss function.
In a previous post, we already discussed the importance of customizing this loss function, for the case of gradient boosting trees. In this post, we shall discuss how to customize the optimizers to speed-up and improve the process of finding a (local) minimum of the loss function.
Optimizers
While the architecture of the Neural Network plays an important role when extracting information from data, all (most) are being optimized through update rules based on the gradient of the loss function.
The update rules are determined by the Optimizer. The performance and update speed may heavily vary from optimizer to optimizer. The gradient tells us the update direction, but it is still unclear how big of a step we might take. Short steps keep us on track, but it might take a very long time until we reach a (local) minimum. Large steps speed up the process, but it might push us off the right direction.
Adam [2] and RMSProp [3] are two very popular optimizers still being used in most neural networks. Both update the variables using an exponential decaying average of the gradient and its squared.
Research has been done into finding new optimizers, either by generating fixed numerical updates or algebraic rules.
Using a controller Recurrent Neural Network, a team [1] found two new interesting types of optimizers, PowerSign and AddSign, which are both performant and require less ressources than the current popular optimizers, such as Adam.
Implementing Optimizers in TensorFlow
Tensorflow is a popular python framework for implementing neural networks. While the documentation is very rich, it is often a challenge to find your way through it.
In this blog post, I shall explain how one could implement PowerSign and AddSign.
The optimizers consists of two important steps:
- compute_gradients() which updates the gradients in the computational graph
- apply_gradients() which updates the variables
Before running the Tensorflow Session, one should initiate an Optimizer as seen below:
# Gradient Descent optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
tf.train.GradientDescentOptimizer is an object of the class GradientDescentOptimizer and as the name says, it implements the gradient descent algorithm.
The method minimize() is being called with a “cost” as parameter and consists of the two methods compute_gradients() and then apply_gradients().
For this post, and the implementation of AddSign and PowerSign, we must have a closer look at this last step apply_gradients().
This method relies on the (new) Optimizer (class), which we will create, to implement the following methods: _create_slots(), _prepare(), _apply_dense(), and _apply_sparse().
_create_slots() and _prepare() create and initialise additional variables, such as momentum.
_apply_dense(), and _apply_sparse() implement the actual Ops, which update the variables. Ops are generally written in C++ . Without having to change the C++ header yourself, you can still return a python wrapper of some Ops through these methods.
This is done as follows:
def _create_slots(self, var_list):
# Create slots for allocation and later management of additional
# variables associated with the variables to train.
# for example: the first and second moments.
'''
for v in var_list:
self._zeros_slot(v, "m", self._name)
self._zeros_slot(v, "v", self._name)
'''
def _apply_dense(self, grad, var):
#define your favourite variable update
# for example:
'''
# Here we apply gradient descents by substracting the variables
# with the gradient times the learning_rate (defined in __init__)
var_update = state_ops.assign_sub(var, self.learning_rate * grad)
'''
#The trick is now to pass the Ops in the control_flow_ops and
# eventually groups any particular computation of the slots your
# wish to keep track of:
# for example:
'''
m_t = ...m... #do something with m and grad
v_t = ...v... # do something with v and grad
'''
return control_flow_ops.group(*[var_update, m_t, v_t])
Let us now put everything together and show the implementation of PowerSign and AddSign.
First, you need the following modules for adding Ops,
# This class defines the API to add Ops to train a model. from tensorflow.python.ops import control_flow_ops from tensorflow.python.ops import math_ops from tensorflow.python.ops import state_ops from tensorflow.python.framework import ops from tensorflow.python.training import optimizer import tensorflow as tf
Let us now implement AddSign and PowerSign. Both optimizers are actually very similar and make use of the sign of the momentum m-hat and gradient g-hat for the update.
PowerSign
For PowerSign the update of the variables w_(n+1) at the (n+1)-th epoch, i.e.,
The decay-rate f_n in the following code is set to 1. I will not discuss this here, and I refer to the paper [1] for more details.
class PowerSign(optimizer.Optimizer):
"""Implementation of PowerSign.
See [Bello et. al., 2017](https://arxiv.org/abs/1709.07417)
@@__init__
"""
def __init__(self, learning_rate=0.001,alpha=0.01,beta=0.5, use_locking=False, name="PowerSign"):
super(PowerSign, self).__init__(use_locking, name)
self._lr = learning_rate
self._alpha = alpha
self._beta = beta
# Tensor versions of the constructor arguments, created in _prepare().
self._lr_t = None
self._alpha_t = None
self._beta_t = None
def _prepare(self):
self._lr_t = ops.convert_to_tensor(self._lr, name="learning_rate")
self._alpha_t = ops.convert_to_tensor(self._beta, name="alpha_t")
self._beta_t = ops.convert_to_tensor(self._beta, name="beta_t")
def _create_slots(self, var_list):
# Create slots for the first and second moments.
for v in var_list:
self._zeros_slot(v, "m", self._name)
def _apply_dense(self, grad, var):
lr_t = math_ops.cast(self._lr_t, var.dtype.base_dtype)
alpha_t = math_ops.cast(self._alpha_t, var.dtype.base_dtype)
beta_t = math_ops.cast(self._beta_t, var.dtype.base_dtype)
eps = 1e-7 #cap for moving average
m = self.get_slot(var, "m")
m_t = m.assign(tf.maximum(beta_t * m + eps, tf.abs(grad)))
var_update = state_ops.assign_sub(var, lr_t*grad*tf.exp( tf.log(alpha_t)*tf.sign(grad)*tf.sign(m_t))) #Update 'ref' by subtracting 'value
#Create an op that groups multiple operations.
#When this op finishes, all ops in input have finished
return control_flow_ops.group(*[var_update, m_t])
def _apply_sparse(self, grad, var):
raise NotImplementedError("Sparse gradient updates are not supported.")
AddSign
AddSign is very similar to PowerSign as seen below,
class AddSign(optimizer.Optimizer):
"""Implementation of AddSign.
See [Bello et. al., 2017](https://arxiv.org/abs/1709.07417)
@@__init__
"""
def __init__(self, learning_rate=1.001,alpha=0.01,beta=0.5, use_locking=False, name="AddSign"):
super(AddSign, self).__init__(use_locking, name)
self._lr = learning_rate
self._alpha = alpha
self._beta = beta
# Tensor versions of the constructor arguments, created in _prepare().
self._lr_t = None
self._alpha_t = None
self._beta_t = None
def _prepare(self):
self._lr_t = ops.convert_to_tensor(self._lr, name="learning_rate")
self._alpha_t = ops.convert_to_tensor(self._beta, name="beta_t")
self._beta_t = ops.convert_to_tensor(self._beta, name="beta_t")
def _create_slots(self, var_list):
# Create slots for the first and second moments.
for v in var_list:
self._zeros_slot(v, "m", self._name)
def _apply_dense(self, grad, var):
lr_t = math_ops.cast(self._lr_t, var.dtype.base_dtype)
beta_t = math_ops.cast(self._beta_t, var.dtype.base_dtype)
alpha_t = math_ops.cast(self._alpha_t, var.dtype.base_dtype)
eps = 1e-7 #cap for moving average
m = self.get_slot(var, "m")
m_t = m.assign(tf.maximum(beta_t * m + eps, tf.abs(grad)))
var_update = state_ops.assign_sub(var, lr_t*grad*(1.0+alpha_t*tf.sign(grad)*tf.sign(m_t) ) )
#Create an op that groups multiple operations
#When this op finishes, all ops in input have finished
return control_flow_ops.group(*[var_update, m_t])
def _apply_sparse(self, grad, var):
raise NotImplementedError("Sparse gradient updates are not supported.")
Performance testing the Optimizers
The Rosenbrock function is a famous performance test for optimization algorithms. The function is non-convex, and defined as,
The resulting shape is plotted in figure (1) below. As we seen, it has a minimum at x = 1 and y = 1.
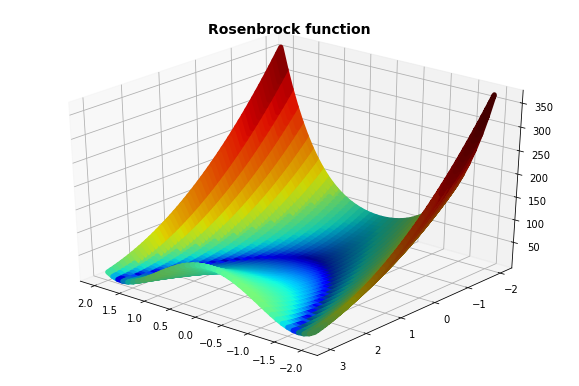
The following script generates the Euclidian distance of the true minimum w.r.t the approximated minimum by a given optimizer at each epoch.
def RosenbrockOpt(optimizer,MAX_EPOCHS = 4000, MAX_STEP = 100):
'''
returns distance of each step*MAX_STEP w.r.t minimum (1,1)
'''
x1_data = tf.Variable(initial_value=tf.random_uniform([1], minval=-3, maxval=3,seed=0),name='x1')
x2_data = tf.Variable(initial_value=tf.random_uniform([1], minval=-3, maxval=3,seed=1), name='x2')
y = tf.add(tf.pow(tf.subtract(1.0, x1_data), 2.0),tf.multiply(100.0, tf.pow(tf.subtract(x2_data, tf.pow(x1_data, 2.0)), 2.0)), 'y')
global_step_tensor = tf.Variable(0, trainable=False, name='global_step')
train = optimizer.minimize(y,global_step=global_step_tensor)
sess = tf.Session()
init = tf.global_variables_initializer()#tf.initialize_all_variables()
sess.run(init)
minx = 1.0
miny = 1.0
distance = []
xx_ = sess.run(x1_data)
yy_ = sess.run(x2_data)
print(0,xx_,yy_,np.sqrt((minx-xx_)**2+(miny-yy_)**2))
for step in range(MAX_EPOCHS):
_, xx_, yy_, zz_ = sess.run([train,x1_data,x2_data,y])
if step % MAX_STEP == 0:
print(step+1, xx_,yy_, zz_)
distance += [ np.sqrt((minx-xx_)**2+(miny-yy_)**2)]
sess.close()
return distance
A performance comparison of each optimizer is plotted below for a run of 4000 epochs.

While the performance heavily vary from the choice of hyperparameters, the extremely fast convergence of PowerSign needs to noticed.
Below, the coordinates of the approximations have been plotted for several epochs.
| Epoch | Rmsprop (x,y,z) | AddSign (x,y,z) | PowerSign (x,y,z) |
|---|---|---|---|
| 0 | (-2.39, -1.57, 4.26) | (-2.39, -1.57, 4.26) | (-2.39, -1.57, 4.26) |
| 501 | (0.66, 0.43, 0.13) | (0.41, 0.17, 0.34) | (0.97, 0.95, 0.0) |
| 1001 | (0.83, 0.67, 0.05) | (0.55, 030, 0.21) | (0.98, 0.96, 0.00) |
| 2001 | (0.93, 0.85, 0.03) | (0.69, 0.48, 0.09) | (0.98, 0.96, 0.00) |
| 3001 | (0.96, 0.92, 0.02) | (0.78, 0.60, 0.05) | (0.98, 0.97, 0.00) |
Final Discussion:
Tensorflow allows us to create our own customizers. Recent progress in research have delivered two new promising optimizers,i.e. PowerSign and AddSign.
The fast early convergence of PowerSign makes it an interesting optimizer to combine with others such as Adam.
References:
- Additional information on PowerSign and AddSign is available on arxiv paper “Neural Optimizer Search with Reinforcement Learning” , Bello et. al., https://arxiv.org/abs/1709.07417.
- Kingma, D. P., & Ba, J. L. (2015). Adam: a Method for Stochastic Optimization. International Conference on Learning Representations, 1–13.
- unpublished
- I have found a lot of useful information through this stackerflow post, which I have attempted to bundle into this post.
Original. Reposted with permission.
Related
