Resampling Imbalanced Data and Its Limits

Can resampling tackle the problem of too few fraudulent transactions in credit card fraud detection?

By Maarit Widmann, Data Scientist at KNIME

Introduction

Car parking ticket machines used to only accept coins. A self-service vegetable stand used to only accept cash. And not such a long time ago I could buy a bus ticket from the bus driver! These days, however, you can (and you’re often encouraged to) pay for these and many other products and services by credit card. This leads to more and more transactions and also to types of transactions that didn’t exist before. Some time back, a credit card transaction for a vegetable stand would have looked suspicious!

With the increasing variety and volume of credit card usage, fraud is evolving too [1]. This is a huge challenge! For automatic fraud detection and prevention, a number of supervised and unsupervised fraud detection models have been suggested. The unsupervised methods, such as a neural autoencoder, are anomaly detection models and don’t require labeled data. The supervised methods, such as a decision tree or a logistic regression model, require labeled data, which are often not available. Imagine someone manually recognizing and labeling the transactions as “fraudulent” or “legitimate”! Another problem is that the fraudulent transactions are very few compared to the large amounts of legitimate transactions. This imbalance of the target classes decreases the performance of the decision tree algorithm and of other classification algorithms [2].

In this article, we will work with labeled, highly imbalanced transactions data: For each fraudulent transaction we have 579 legitimate transactions. We’ll check if we can improve the performance of a decision tree model by resampling; that is, by artificially creating more data about fraudulent transactions. Along the way, we’ll explain three different resampling methods and evaluate their effects on the fraud prevention application. At the end, we’ll provide a link to a KNIME workflow - an example implementation of the different resampling methods.

Building a Classification Model for Fraud Detection

In our demonstration we use the creditcard.csv data available on Kaggle. The data consist of 284807 credit card transactions, performed by EU cardholders in September 2013. 492 (0.2%) of the credit card transactions are fraudulent, and the remaining 284315 (99.8%) transactions are legitimate. The data contain a target class column with possible values fraudulent / legitimate, the time and amount of each transaction, and 28 principal components generated from the confidential features of the transactions.

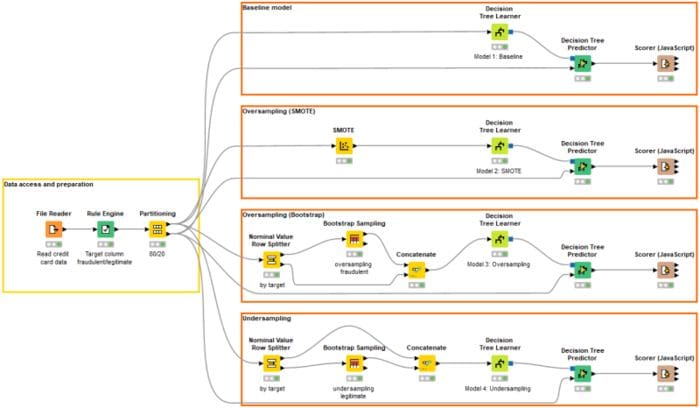
The workflow in Figure 1 shows the steps for accessing, preprocessing, resampling, and modeling the transactions data. Inside the yellow box, we access the transactions data, encode the target column from 0/1 to legitimate/fraudulent, and partition the data into training and test sets using 80/20 split and stratified sampling on the target column. Inside the orange boxes, we build four different versions of a decision tree model for fraud detection: a baseline model trained on the original training data plus three models trained on

SMOTE oversampled data,
Bootstrap oversampled data, and
Bootstrap undersampled data.

Figure 1. A workflow that accesses and preprocesses transactions data and implements four different decision tree models for fraud detection: one trained on the original data and three models trained on resampled data.

Resampling Techniques

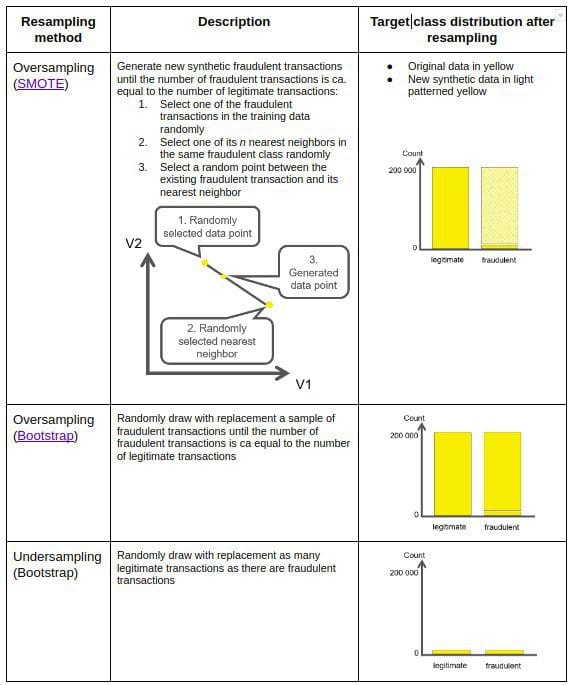
Table 1 summarizes the resampling methods that we include in our demonstration:

oversampling (SMOTE)
oversampling (Bootstrap)
undersampling (Bootstrap)

Table 1. Overview of three resampling methods: SMOTE, oversampling (Bootstrap), and undersampling (Bootstrap)

Effects of Resampling on Fraud Detection Performance

Resampling has two drawbacks, especially when the target class is as highly imbalanced as in our case. Firstly, oversampling the minority class might lead to overfitting, i.e. the model learns patterns that only exist in the particular sample that has been oversampled. Secondly, undersampling the majority class might lead to underfitting, i.e. the model fails to capture the general pattern in the data [3].

We compare the performances of the baseline model and the models trained on resampled data in terms of two scoring metrics: recall and precision (Figure 2). The metrics are explained in detail in the From Modeling to Scoring: Confusion Matrix and Class Statistics blog post.

Recall is the proportion of correctly predicted fraudulent transactions. The higher the recall, the more fraudulent transactions are prevented by the model.
Precision is the proportion of actual fraudulent transactions among those predicted as fraudulent. The higher the precision, the fewer false alarms are raised by the model.

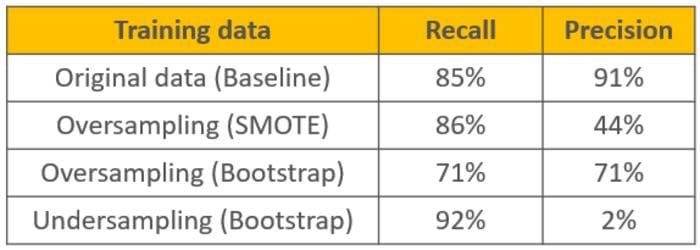
Figure 2. Recall and precision statistics obtained by four decision tree models for fraud detection, each one trained on a different training set

The very low precision value 2% for the undersampled model in the bottom right corner in Figure 2 indicates underfitting: The undersampled model failed to learn the patterns underlying the legitimate transactions. This seems reasonable considering that we discarded 99.8% of the legitimate transactions in the undersampling phase! Indeed, with so few examples in the fraudulent class, the only effect of undersampling has been to damage the representation of the legitimate class.

If you take a look at the performances obtained via oversampling in the two middle rows, you can see from their precision value that these models are raising more false alarms than the model trained on the full original data, while at the same time not improving the recognition of the pattern underlying the fraudulent transactions. All of this indicates that the model has overfitted the data.

As you can see, our fraud detection model is over-/underfitting when trained on resampled data. What is actually happening under the hood?

Demonstrating Over- and Underfitting in Fraud Detection

Transactions data are confidential, and we can therefore only work with principal components as predictors of the target class fraudulent/legitimate. In order to better understand how a resampled model leads to over- or underfitting, let’s imagine we had some of the following columns in our data, since they often characterize fraudulent transactions [4]:

Shipping address equals billing address: yes/no
Urgent delivery: yes/no
Number of different items in the order
Number of orders of the same item
Number of credit cards associated with the shipping address

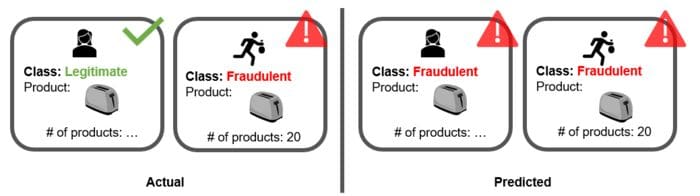
Since our training data only contain 394 fraudulent transactions, it could be, for example, that the majority of them are characterized by exceptionally many orders of the same item: one for 20 toasters, another for 50 smartphones, yet another for 25 winter coats, and so on. In reality, the fraudulent transactions are much more varying and continuously evolving. On the contrary, the 227451 legitimate transactions in the training data represent a huge variety of ways of using the credit card: for a banana, hotel booking, toaster, car parking, and more!

In the following, we explain how the different resampling methods skew the transactions data, and how this leads to a deterioration in model performance, as we saw before.

Oversampling (SMOTE)

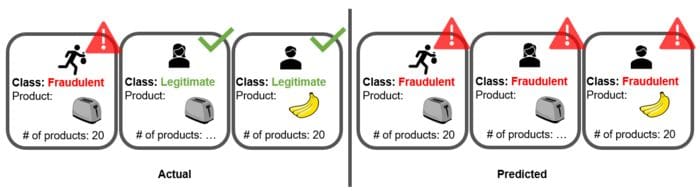
The corresponding model has a low precision value (44%) and it therefore raises many false alarms. The training set contains the original fraudulent transactions plus the synthetically generated fraudulent transactions within the feature space of the fraudulent transactions. For example, if we had one fraudulent transaction that purchases 20 toasters, SMOTE resampling might produce thousands of slightly different fraudulent transactions that all purchase a toaster. Eventually, all legitimate transactions that include a toaster would be predicted as fraudulent. This kind of model is overfitting the training data (Figure 3).

Figure 3. Example class predictions generated by an overfitting fraud detection model trained on SMOTE oversampled data: An arbitrary feature, for example, product=toaster incorrectly determines fraudulent transactions in new data.

Oversampling (Bootstrap)

This model performs worse than the baseline model in terms of both recall and precision. The training set contains thousands of exact copies of the original fraudulent transactions. For example, if we had a fraudulent transaction ordering 20 toasters, all legitimate transactions that ordered 20 items of the same product or a toaster would be suspicious, because these two features would have characterized so many fraudulent transactions in the oversampled data. At the same time, the model would have failed to generalize on large amounts of the same item as suspicious, emphasizing instead precisely 20 toasters as suspicious. Also this model is overfitting the training data (Figure 4).

Figure 4. Example class predictions generated by an overfitting fraud detection model trained on Bootstrap oversampled data: an arbitrary set of features, for example, product=toaster and # of products=20 incorrectly determines fraudulent transactions in new data.

Undersampling (Bootstrap)

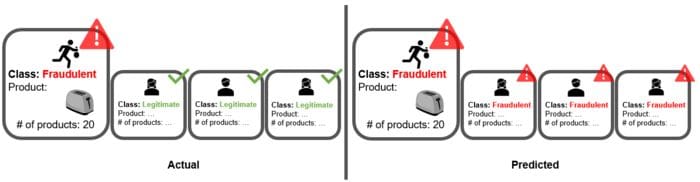
The model performs almost perfectly in terms of recall (92%), yet the worst in terms of precision (2%). Since more than 99% of the original transactions are discarded in the undersampling phase, our training data might only consist of credit card transactions for food and leave out hotel bookings, car parking, and many others. This kind of training data is not representative of the real data. Therefore, almost all transactions are predicted as fraudulent; the model is underfitting (Figure 5).

Figure 5. Example class predictions generated by an underfitting fraud detection model trained on Bootstrap undersampled data: the model predicts all transactions as fraudulent in new data.

Diagnosing Problems of Resampling in Fraud Detection

As our example shows, in this case resampling can’t solve the problem of having too few fraudulent transactions in the dataset. However, resampling is shown to lead to performance gain when the a priori distribution is less skewed, for example, in disease detection [5]. Why is resampling failing then, for this credit card transaction dataset with too few fraudulent transactions in it?

Frauds are perpetrated in a large variety of patterns, and we have only a few fraudulent transactions in our training data. So fraud patterns are definitely under-represented in our training set. Resampling doesn’t solve the problem, because it does not increase the variety of the representation of fraudulent transactions, it just replicates in some form the fraud patterns represented in the dataset. Thus, the models trained on resampled data can only perform well in detecting some types of fraud, the types represented in the training data.

In summary, the class of fraudulent transactions is too under-represented (just 0.2% of the whole dataset!) to represent a meaningful description of all the fraud patterns that are out there. Even introducing new similar synthetic fraudulent transactions cannot significantly change the range of the represented fraudulent transactions.

Conclusions

Transactions data are produced in huge volumes every day. In order to build a supervised model for fraud detection, they would need to be labeled. The labeling process, however, in this case, is tricky.

Firstly, even if we had the knowledge to appropriately label fraudulent transactions, the process would be very resource-intensive. Skillful experts at detecting frauds are rare and expensive and usually do not spend their time labeling datasets. Even with reliable and sufficient resources, manual labeling would take a prohibitively long time before a sufficiently large amount of data would be available.

Secondly, expertise in fraud detection is so scarce, because criminals creatively devise ever newer fraud schemes and it is hard to keep up the pace with the newly introduced patterns. An expert might recognize all types of frauds known till then and still fail at recognizing the new fraud schemes, most recently created.

Finally, and luckily, there are generally fewer fraudulent transactions than legitimate transactions. Even after all this manual effort by extremely skillful people, we might still end up with an insufficient number of data for the fraudulent class.

Those are all reasons why fraud detection is often treated as a rare class problem, rather than an imbalanced class problem.

Yet, we can try. With this dataset, can we artificially increase the sample size of fraudulent transactions by resampling the training data? Not really. Resampling can improve the model performance if the target classes are imbalanced and yet sufficiently represented. In this case, the problem is really the lack of data. Resampling is subsequently leading to over- or underfitting rather than to a better model performance.

This article just aims at giving you an idea of why, in some cases, resampling cannot work. Of course, better results could be obtained with more sophisticated resampling methods than those we have introduced in this article, like for example, a combination of under- and oversampling [6]. Better results could also be obtained with supervised algorithms other than the decision tree. Some machine learning supervised algorithms, such as logistic regression, are less sensitive to class imbalance than the decision tree, while other algorithms, such as ensemble models, are more robust to overfitting. Even better results could be obtained with the decision tree, for example by applying pruning techniques to avoid the overfitting effect or controlling the tree growth.

However, sometimes we must accept that the data is just not sufficient to describe the minority class. In this case, we must proceed with unlabeled data and try to isolate the events of the rare class via unsupervised algorithms, such as neural autoencoders, isolation forest, and clustering algorithms.

The Resampling in Supervised Fraud Detection Models workflow, used in this article to show the limitations of resampling, can be downloaded for free from the KNIME Hub.

References

[1]"The Nilson Report." HSN Consultants, Inc., November 2019, Issue 1164, https://nilsonreport.com/publication_newsletter_archive_issue.php?issue=1164. Accessed 14 Oct. 2020.
[2]"Random Oversampling and Undersampling for Imbalanced Classification" Machine Learning Mastery Pty. Ltd., January 2020, https://machinelearningmastery.com/random-oversampling-and-undersampling-for-imbalanced-classification/. Accessed 14 Oct. 2020.
[3]"Oversampling and Undersampling" Medium, September 2010, https://towardsdatascience.com/oversampling-and-undersampling-5e2bbaf56dcf. Accessed 14 Oct. 2020.
[4]https://www.bluefin.com/support/identifying-fraudulent-transactions/
[5]"Machine Learning Resampling Techniques for Class Imbalances" Medium, January 2011, https://towardsdatascience.com/machine-learning-resampling-techniques-for-class-imbalances-30cbe2415867. Accessed 14 Oct. 2020.
[6]"How to Combine Oversampling and Undersampling for Imbalanced Classification" Machine Learning Mastery Pty. Ltd., January 2020, https://machinelearningmastery.com/combine-oversampling-and-undersampling-for-imbalanced-classification/. Accessed 14 Oct. 2020.

Bio: Maarit Widmann is a Data Scientist at KNIME.

Related: