What is Structural Equation Modeling?

Structural Equation Modeling (SEM) is an extremely broad and flexible framework for data analysis, perhaps better thought of as a family of related methods rather than as a single technique. Its origins can be traced back to Psychologist Charles Spearman at the turn of the 20th century and Geneticist Sewall Wright in the immediate aftermath of WWI. Many others have had a hand in its development, notably Karl Jöreskog and Peter Bentler. Covariance Structure Analysis and LISREL, the name of a program Jöreskog co-developed, are other terms occasionally used interchangeably with Structural Equation Modeling.

What is its relevance to Marketing Research? Attitudes, opinions and personality traits are important drivers of consumer behavior, but they are latent constructs and marketing researchers cannot actually observe them or measure them directly. We can only make inferences about them from what we can observe, responses to questionnaire items, for example. Measuring latent constructs is challenging and we must also incorporate estimates of measurement error into our models. SEM excels at both of these tasks.

Put very simply, SEM simultaneously unites Factor Analysis and Regression but offers the modeler with much more flexibility than either of these two techniques. It is not the same as running a Factor Analysis and then inputting factor scores into a Multiple Regression. SEM is especially suited for causal analysis. Also, when multicollinearity - highly correlated independent variables - is a concern, SEM is the tool of choice for many researchers.

The part of SEM analogous to Factor Analysis is called the measurement model, and the elements that tie the components of the measurement model together or relate them to one or more dependent variables is called the structural model. Sometimes, however, variables are combined ("parceled") on empirical or theoretical grounds prior to analysis and the measurement model plays no role. At other times we are not concerned with measurement error and only the raw variables - "observed variables" in SEM jargon - are used. When there is no measurement model - only the structural model - the term Path Analysis is more appropriate than SEM, though some use "SEM" very generally.

Though often used to analyze survey data, it is not restricted to any one data source and can be used with social media data, customer transaction data, economic data and is even used in Neuroscience for analysis of fMRI data. In its modern forms it is able to be used with any data type - ratio, interval, ordinal, nominal and count - and can model curvilinear relationships among variables as well as interactions.

It does not require complete data...though missing data should never be treated cavalierly! It is increasingly used for Hierarchical, Mixed and Longitudinal Modeling, and can also be used in Segmentation. It can accommodate multiple dependent variables and is sometimes blended with Conjoint Analysis. SEM can also be used to adjust for individual response styles in consumer surveys and other questionnaire data. For the technically-inclined among you, SEM can be estimated with Maximum Likelihood or Bayesian approaches.

Out of breath? Don't worry - the hard part of this post is now over!

When do we use it?

 
Imagine if you wanted to better understand which consumer perceptions are most strongly associated with Liking, Purchase Interest or Satisfaction in your product or service category, and also see if there are latent segments (clusters) of consumers with different perceptions of the category or features they are seeking. Though not a simple modeling task, SEM would be appropriate for these objectives, and the images of brands could also be mapped to help us understand how the dimensions underlying brand perceptions distinguish the brands.

SEM can be used for simpler jobs, such as the example below from a consumer survey on a men's personal care category. This illustration is a simplified and cloaked version of the full model, which included many more attributes as well as exogenous variables such as age. I should note that a great deal of output besides a path diagram needs to be checked carefully!

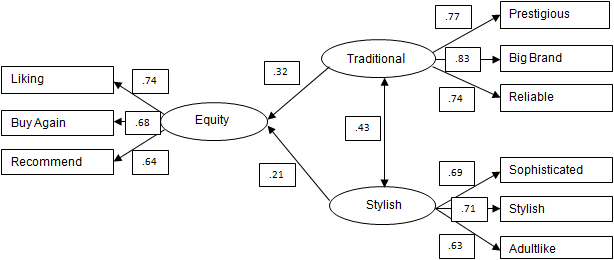
• In the path diagram above, ovals represent factors, also known as latent variables, unobserved variables or unmeasured variables in SEM lingo. These are theoretical concepts which can be inferred but not directly measured.
• Rectangles are used to represent attributes, also called measured variables, observed variables, or manifest variables. In this example, the Traditional factor is represented by, or measured by, the attributes Prestigious, Big Brand and Reliable.
• Single-headed arrows pointing from one latent variable to another depict hypothetical causal relationships, for instance the impact of Traditional on Brand Equity, the dependent variable in this analysis. These can be likened to regression coefficients. The single-headed arrows running from the latent variables to the attributes are equivalent to loadings in Factor Analysis.
• The double-headed arrow is the correlation between the latent exogenous (independent) variables in this example. 
• The numbers adjacent the arrows are the regression coefficients, correlation coefficients and factor loadings. In SEM, regression coefficients are normally smaller than correlations and loadings, as they are here.
• To reduce clutter, I've omitted error and residual terms, which are similar to unique factors in Factor Analysis and residual terms in regression.

The brands rated in this survey were also mapped in a scatterplot according to their factor scores in the full model. This is not shown for reasons of confidentiality and space.

Structural Equation Mixture Modeling (SEMM) was employed to see if there might be hidden segments of consumers with very different needs lurking in the data. (I call this "Driver Segmentation.") It was concluded that two driver models were needed, which partly reflected price tier, but that the same factors (latent variables) could be used for these two segments. This is not always the case and there are times when entirely different models are necessary.

Merely assuming that a one-size-fits-all model is sufficient can lead to very bad decisions, but running many models on pre-determined subgroups is also ill-advised unless we have sound theoretical and empirical grounds to believe these subgroups are truly distinct with regard to their needs or perceptions. Mixture Modeling is very tricky but worth the effort when done competently. Sometimes we conclude that one overall model is sufficient - negative findings are also important.

A few FAQs

 
How big a sample do I need? Two guidelines cited over the years are a minimum of 200 cases (e.g., survey respondents) and at least 10 cases per measured variable (e.g., 250 respondents if there are 25 attribute ratings in the model). These guidelines are merely rules of thumb, however, and now questioned by many authorities.

What about Big Data? SEM has only begun to migrate outside its birthplaces - primarily Psychology, Sociology and Education - in the past 10-15 years. I remember reading an article in the Journal of the American Statistical Association introducing the method to its readership. This was in 2006, if I recall correctly, long after SEM had been in use in the social and behavioral sciences. It is still underutilized in Marketing Research, in my opinion, as are advanced analytics generally.

Data Scientists only now seem to be catching wind of SEM. It is not a computationally fast procedure but on today's hardware does work well on quite large samples with many variables. "Big" is relative! In some circumstances it makes sense to use a standard machine learning tool such as LogitBoost for predictions and SEM on a sample of the same data to try to understand the mechanism generating the data - The Why in marketingspeak.

What statistical assumptions do I need to make? This is very case-by-case, depending on the type of SEM model you run. SEM, like most statistical procedures, is quite robust to violations of assumptions and standard errors are more vulnerable than the coefficient estimates, generally speaking.

I've heard that SEM can only be used to test hypotheses. Is this true? This is a common misconception about statistics, not just SEM. Theories don't just pop out of thin air and very often are developed on the basis of observations. Put simply, we see things happening and we try to figure out why they are happening. That said, exploratory analysis - even if you're just using cross tabs - carries with it a high risk of findings that won't replicate or generalize beyond a sample or very narrow population. We always need to be careful and do our homework.

How do I know my model is any good? A wide variety of fit indices are used for this. The Comparative Fit Index (CFI) and the Root Mean Square Error of Approximation (RMSEA) are perhaps most common. The more familiar R squared is sometimes informative as well. I should stress, though, that whether the model is "good enough" will ultimately depend on commonsense, relevant theory and potential utility to decision-makers. To a large degree, it's a judgement call.

Further Reading

 
There is a great deal of material about SEM online, as well as seminars and university courses on SEM or that include it as a major topic. Barbara M. Byrne has written some extremely readable introductory books focused on widely-used commercial SEM statistical packages (e.g., Structural Equation Modeling with EQS). Slightly more advanced but also very readable is the popular book by Rex B. Kline entitled  Principles and Practice of Structural Equation Modeling.

Structural Equations with Latent Variables (Bollen) is the "classic" text that lays bare the mathematical foundations of SEM. Linear Causal Modeling with Structural Equations by Stan Mulaik is similar to Bollen's but newer and more concentrated on causal analysis, a major application of SEM, as noted. Handbook of Structural Equation Modeling (Hoyle) is a dense and comprehensive volume that covers all the major SEM topics.

A Primer on Partial Least Squares Structural Equation Modeling (Hair et al.) and Causality: Models, Reasoning and Inference (Pearl) introduce PLS and Bayesian Networks, respectively, two methods that are seen by some researchers as alternatives to SEM.

Structural Equation Modeling: A Multidisciplinary Journal (Routledge) is the preeminent academic journal on SEM and SEMNET is an electronic mail network about SEM. I've listed many other books on SEM and associated topics in my company library.

A good background in Psychometrics will help you take full advantage of SEM. Psychometrics: An Introduction (Furr and Bacharach) and Introduction to Psychometric Theory (Raykov and Marcoulides) are two recent texts that will get you started if you're new to the discipline. The second of these is quite a bit more advanced than the first.

To sum up...

 
"With power comes responsibility" comes to mind first and foremost when I think of SEM. It's a powerful tool that, statistically speaking, is also very dangerous. Though SEM is technically very complex, it's quite easy to point-and-click ourselves into very awkward situations with today's user-friendly software.

Many models may provide similar fits to the data but suggest very different interpretations and courses of action for decision makers. In addition, we need to be careful about not overfitting, very easy to do with SEM. I've also been in situations in which I was "encouraged" to run model after model until I found one that suited the internal politics of the client...there is a human element to statistical modeling that does not always receive the attention it should.

An important area of Marketing Research falls in between purely qualitative research and hard, quantitative research, and SEM is particularly nimble in this grey space. I personally find this kind of MR fascinating, and know from having worked in the field for more than 30 years just how critical it is to decision makers.

I hope you've found this interesting and helpful!

Bio: Kevin Gray is president of Cannon Gray, a marketing science and analytics consultancy.

Related:

• Neuroscience for Data Scientists: Understanding Human Behaviour
• Proxy Indicators: beware of spurious claims
• Time Series Analysis: A Primer