A First Principles Theory of Generalization

Source: The Singularity Hub

I recently started a new newsletter focus on AI education and already has over 50,000 subscribers. TheSequence is a no-BS( meaning no hype, no news etc) AI-focused newsletter that takes 5 minutes to read. The goal is to keep you up to date with machine learning projects, research papers and concepts. Please give it a try by subscribing below:

Most of machine learning(ML) papers we see these days are focused on advancing new techniques and methods in different areas such as natural language or computer vision. ML research is advancing at a frantic pace despite the lack of fundamental theory of machine intelligence. Some of the main questions in ML such as how to understand how neural networks learn or how to quantify knowledge generalization remain unanswered. From time to time, we come across papers that are challenging our fundamental understanding of ML theory with new ideas. This is the case of “Neural Tangent Kernel Eigenvalues Accurately Predict Generalization”, a groundbreaking paper just published by Berkeley AI Research(BAIR) that proposes nothing less that a new theory of generalization.

Understanding generalization remains one of the biggest mysteries in modern ML. In their paper, the BAIR researchers tackle an variation of the fundamental question of generalization stated in the following statement:

Can one efficiently predict, from first principles, how well a given network architecture will generalize when learning a given function, provided a given number of training examples?

To answer this question, the BAIR team relied on two recent breakthroughs in deep learning:

1) Infinite-Width Networks

 
 
One of the most interesting theoretical developments in the recent years of deep learning is the theory of infinite-width networks. This development states that, as hidden layers in a neural network tend to infinite, the behavior of the neural network itself takes a very simple analytical forms. This idea suggest that, by studying theoretically infinite neural networks, we can gain insights into the generalization of the finite equivalent. This is similar to the central limit theorem in traditional calculus.

2) Kernel Regression Approximations

 
 
The second breakthrough is tightly related to the first one but it goes more into specifics. Recent research in deep learning optimization suggests a wide network trained by gradient descent with mean-squared-error (MSE) loss is equivalent to a classical model called kernel regression. In this case, the kernel is the network’s “neural tangent kernel” (NTK) which describes its evolution when trained using gradient descent. In more normal terms, research suggests that an approximation for the MSE of kernel regressions( with NTK as the kernel) that can accurately predict the MSE of networks learning arbitrary functions.

Learnability

 
 
The biggest contribution of BAIR’s first-principles theory of generalization is the concept of learnability. The idea of learnability is to quantify the approximation between the target and learned functions. That sounds awfully familiar to MSE but learnability exhibits different properties than MST which makes it a better fit for later models.

In the following figure, we can see the results of four different neural networks represented by different colors trained with different training size. The curves represent the theoretical predictions and the dots the true performance. We can see that the learnability metrics align much better.

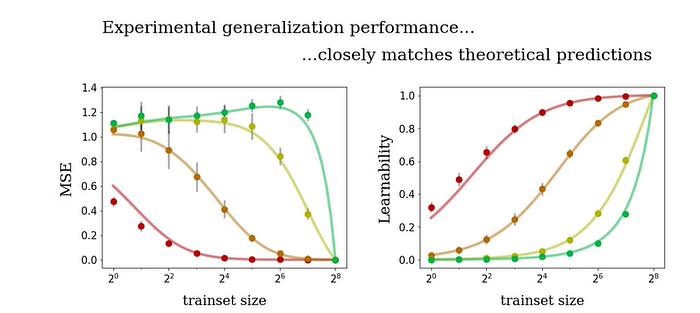
Image Credit: BAIR

The results from the BAIR research are far from conclusive but show that there is more work to be done in order to arrive to a general theory of neural network generalization. The contribution of the learnability metric shows that simple improvements in the traditional MSE and kernel regression methods can lead to much accurate understanding of how neural networks generalize knowledge. By going back to first principles.

 
Bio: Jesus Rodriguez is currently a CTO at Intotheblock. He is a technology expert, executive investor and startup advisor. Jesus founded Tellago, an award winning software development firm focused helping companies become great software organizations by leveraging new enterprise software trends.

Original. Reposted with permission.

Related:

• How Reading Papers Helps You Be a More Effective Data Scientist
• Learn To Reproduce Papers: Beginner’s Guide
• Neural Networks from a Bayesian Perspective