Graph theory might sound like an intimidating and abstract topic to you, so why should you even spend your time reading an article about it? However, although it might not sound very applicable, there are actually an abundance of useful and important applications of graph theory! In this article, I will try to explain briefly what some of these applications are. In doing so, I will do my best to convince you that having at least some basic knowledge of this topic can be useful in solving some interesting problems you might come across.
In this article, I will through a concrete example show how a route planning/optimization task can be formulated and solved using graph theory. More specifically, I will consider a large warehouse consisting of 1000s of different items in various locations/pickup points. The challenge here is, given a list of items, which path should you follow through the warehouse to pickup all items, but at the same time minimize the total distance traveled? For those of you familiar with these kind of problems, this has quite some resemblance to the famous traveling salesman problem. (A well known problem in combinatorial optimization, important in theoretical computer science and operations research).
As you might have realized, the goal of this article is not to give a comprehensive introduction to graph theory (which would be quite a tremendous task). Through a real-world example, I will rather try to convince you that knowing at least some basics of graph theory can prove to be very useful!
I will start with a brief historical introduction to the field of graph theory, and highlight the importance and the wide range of useful applications in many vastly different fields. Following this more general introduction, I will then shift focus to the warehouse optimization example discussed above.
The history of Graph Theory
The basic idea of graphs were first introduced in the 18th century by the Swiss mathematician Leonhard Euler, one of the most eminent mathematicians of the 18th century (and of all time, really). His work on the famous “Seven Bridges of Königsberg problem”, are commonly quoted as origin of graph theory.
The city of Königsberg in Prussia (now Kaliningrad, Russia) was set on both sides of the Pregel River, and included two large islands — Kneiphof and Lomse — which were connected to each other, or to the two mainland portions of the city, by seven bridges (as illustrated in the below figure to the left). The problem was to devise a walk through the city that would cross each of those bridges once and only once.
Euler, recognizing that the relevant constraints were the four bodies of land & the seven bridges, drew out the first known visual representation of a modern graph. A modern graph, as seen in bottom-right image, is represented by a set of points, known as vertices or nodes, connected by a set of lines known as edges.
This abstraction from a concrete problem concerning a city and bridges etc. to a graph makes the problem tractable mathematically, as this abstract representation includes only the information important for solving the problem. Euler actually proved that this specific problem has no solution. However, the difficulty he faced was the development of a suitable technique of analysis, and of subsequent tests that established this assertion with mathematical rigor. From there, the branch of math known as graph theory lay dormant for decades. In modern times, however, it’s applications are finally exploding.
Introduction to Graph Theory
As mentioned previously, I do not aim to give a comprehensive introduction to graph theory. The following section still contains some of the basics when it comes to different kind of graphs etc., which is of relevance to the example we will discuss later on path optimization.
Graph Theory is ultimately the study of relationships. Given a set of nodes & connections, which can abstract anything from city layouts to computer data, graph theory provides a helpful tool to quantify & simplify the many moving parts of dynamic systems. Studying graphs through a framework provides answers to many arrangement, networking, optimization, matching and operational problems.
Graphs can be used to model many types of relations and processes in physical, biological, social and information systems, and has a wide range of useful applications such as e.g.
- Finding communities in networks, such as social media (friend/connection recommendations), or in the recent days for possible spread of COVID19 in the community through contacts.
- Ranking/ordering hyperlinks in search engines.
- GPS/Google maps to find the shortest path home.
- Study of molecules and atoms in chemistry.
- DNA sequencing
- Computer network security
- ….. and many more….

As mentioned, there are several types of graphs that describe different kind of problems (and the constraints within them). A nice walk-through of various types of graphs can also be found in a previous article by Kelvin Jose, and the below section represents a subset of that article.
Types of Graphs
There are different types of graph representations available and we have to make sure that we understand the kind of graph we are working with when programmatically solving a problem which includes graphs.
- Undirected Graphs
As the name shows, there won’t be any specified directions between nodes. So an edge from node A to B would be identical to the edge from B to A.
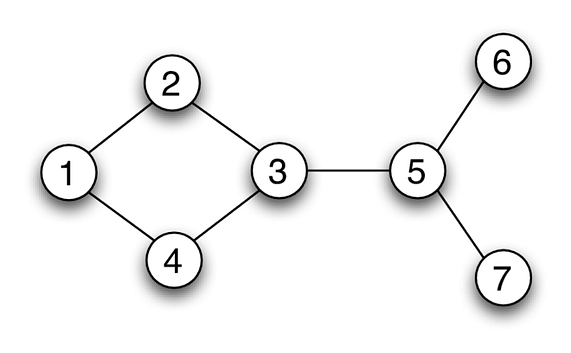
In the above graph, each node could represent different cities and the edges show the bidirectional roads.
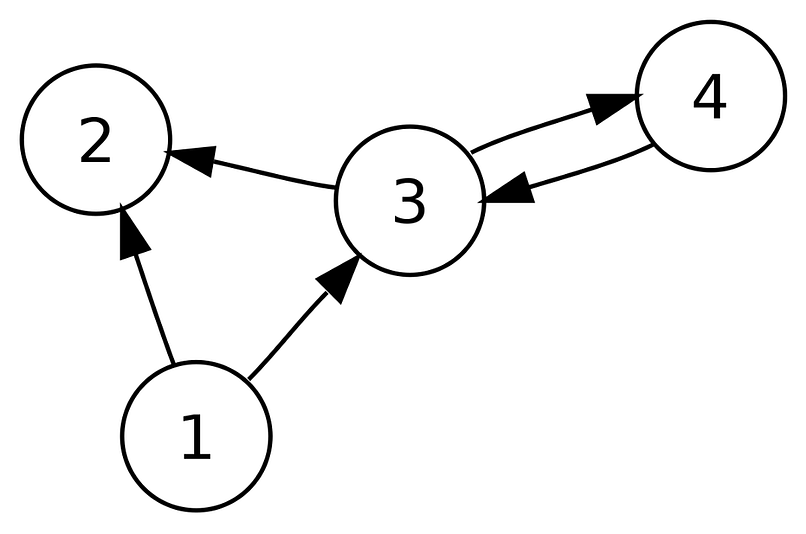
- Directed Graphs (DiGraphs)
Unlike undirected graphs, directed graphs have orientation or direction among different nodes. That means if you have an edge from node A to B, you can move only from A to B.
Like the previous example, if we consider nodes as cities, we have a direction from city 1 to 2. That means, you can drive from city 1 to 2 but not back to city 1, because there is no direction back to city 1 from 2. But if we closely examine the graph, we can see cities with bi-direction. For example cities 3 and 4 have directions to both sides.
- Weighted Graphs
Many graphs can have edges containing a weight associated to represent a real world implication such as cost, distance, quantity etc …
Weighted graphs could be either directed or undirected graph. The one we have in this example is an undirected weighted graph. The cost (or distance) from the green to the orange node (and vice versa) is 3. Like our previous example, if you want to travel between two cities, say city green and orange, we would have to drive 3 miles. These metrics are self-defined and could be changed according to the situations. For a more elaborated example, consider you have to travel to city pink from green. If you look at the city graph, we can’t find any direct roads or edges between the two cities. So what we can do is to travel via another city. The most promising routes would be starting from green to pink via orange and blue. If the weights are costs between cities, we would have to spend 11$ to travel via blue to reach pink but if we take the other route via orange, we would only have to pay 10$ for the trip.
There may be several weights associated with each edge, including distance, travel time, or monetary cost. Such weighted graphs are commonly used to program GPS’s, and travel-planning search engines that compare flight times and costs.
Graph Theory → Route optimization
Having (hopefully) convinced you that graph theory is worth knowing something about, it is now time to focus on our example case of route planning when picking items in our warehouse.
Challenge:
The challenge here is that given a “picking list” as input, we should find the shortest route that passes all the pickup points, but also complies to the restrictions with regard to where it is possible/allowed to drive. The assumptions and constraints here are that crossing between corridors in the warehouse is only allowed at marked “turning points”. Also, the direction of travel must follow the specified legal driving direction for each corridor.
Solution:
This problem can be formulated as an optimization problem in graph theory. All pickup points in the warehouse form a “node” in the graph, where the edges represent permitted lanes/corridors and distances between the nodes. To introduce the problem more formally, let us start from a simplified example.
The graph below represents 2 corridors with 5 shelves/pickup-points per corridor. All shelves are here represented as a node in the graph, with an address ranging from 1–10. The arrows indicate the permitted driving direction, where the double arrows indicate that you can drive either way. Simple enough, right?

Being able to represent the permitted driving routes in the form of a graph, means that we can use mathematical techniques known from graph theory to find the optimal “driving route” between the nodes (i.e., the stock shelves in our warehouse).
The example graph above can be described mathematically through an «adjacency matrix». The adjacency matrix to the right in the below figure is thus a representation of our «warehouse graph», which indicates all permitted driving routes between the various nodes.

- Example 1: You are allowed to travel from node 2 → 3, but not from 3 → 2. This is indicated by the “1” in the adjacency matrix to the right.
- Example 2: You are allowed to go from both node 8 → 3, and from 3 → 8, again indicated by the “1”`s in the adjacency matrix (which in this case is symmetric when it comes to travel direction).
Back to our warehouse problem:
A real warehouse is of course bigger and more complex than the above example. However, the main principles of how to represent the problem through a graph remains the same. To make the real problem slightly simpler (and more visually suitable for this article), I have reduced the total number of shelves/pickup-points (approximately every 50th shelf included, marked with black squares in the below figure). All pickup points are given an address (“node number”) from 1–74. The other relevant constraints mentioned earlier, such as permitted driving directions in each of the corridors, as well as the allowed “turning points” and shortcuts between the corridors are also indicated in the figure..

The next step is then to represent this graph in the form of a adjacency matrix. Since we are here interested in finding both the optimal route and total distance, we must also include the driving distance between the various nodes in the matrix.
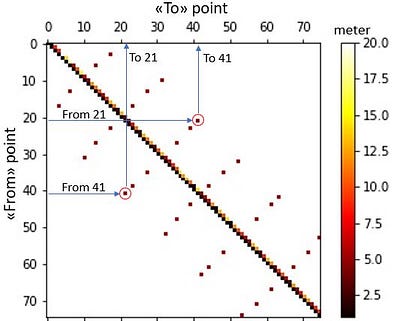
This matrix indicates all constraints with regard to both the permitted direction of travel, which “shortcuts” are permitted, any other restrictions as well as the driving distance between the nodes (illustrated through the color). As an example, the “shortcut” between nodes 21 and 41 shown in the graph representation can clearly be identified also in the adjacency matrix. The “white areas” of the matrix represents the paths that are not allowed, indicated through an “infinite” distance between those nodes.
From graph representation to path optimization
Just having an abstracted representation of our warehouse in the form of a graph, does of course not solve our actual problem. The idea is rather that through this graph representation, we can now use the mathematical framework and algorithms from graph theory to solve it!
Since graph optimization is a well-known field in mathematics, there are several methods and algorithms that can solve this type of problem. In this example case, I have based the solution on the “Floyd-Warshall algorithm”, which is a well known algorithm for finding shortest paths in a weighted graph. A single execution of the algorithm will find the lengths (summed weights) of shortest paths between all pairs of nodes. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm.
If you give this algorithm as input a “picking order list” where you go through a list of items you want to pick, you should then be able to obtain the optimal route which minimize the total driving distance to collect all items on the list.
Example: Let us start by visualizing the results for a (short) picking list as follows: Start from node «0», pick up items at location/node 15, 45, 58 and 73 (where these locations are illustrated in the figure below). The algorithm finds the shortest allowable route between these points through calculating the “distance matrix”, D, which can then be used to determine the total driving distance between all locations/nodes in the picking list.
- Step 1: D[0][15] → 90 m
- Step 2: D[15][45] →52 m
- Step 3: D[45][58] → 34 m
- Step 4: D[58][73] → 92 m
Total distance = 268m
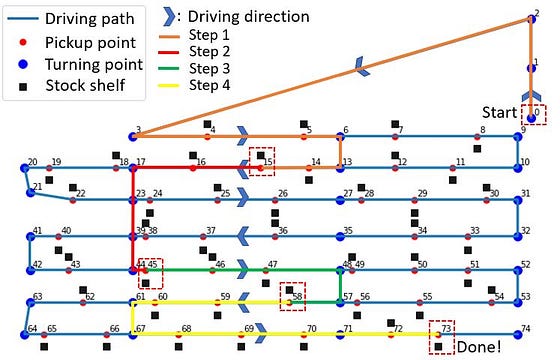
Have tested several “picking lists” as input and verifying the proposed driving routes and calculated distance, the algorithm has been able to find the optimal route in all cases. The algorithm respects all the imposed constraints, such as the permitted direction of travel, and uses all permitted “shortcuts” to minimize the total distance.
From path optimization to useful insights
As shown through the above example, we have developed an optimization algorithm that calculates the optimal driving route via all points on a picking order list (for a simplified version of the warehouse). By providing a list of picking orders as input, one can thus relatively easily calculate statistics on typical mileage per. picking order. These statistics can then also be filtered on various information such as item type, customer, date, etc. In the following section, I have thus picked a few examples on how one can extract interesting statistics from such a path optimization tool.
In doing this, I first generated 10.000 picking order lists where the number of items per list ranges from 1–30 items, located at random pickup points in the warehouse (address 3–74 in the figure above). By performing the path optimization procedure over all these picking list, we can then extract some interesting statistics.
Example 1: Calculate mileage as a function of the number of units per. picking order list. Here, you would naturally assume that the total mileage increases the more items you have to pick. But, at some level, this will start to flatten out. This is due to the fact that one eventually has to stop by all the corridors in the warehouse to pick up goods, which then prevents us from making use of clever “shortcuts” to minimize the total driving distance. This tendency can be illustrated in the figure below to the left, which illustrates that for more than approximately 15–20 units per picking order, adding extra items does not make the total mileage much longer (as you have to drive through all corridors of the warehouse anyway). Note that the figures show a “density plot” of the distribution of typical mileage per. picking orders list.
Another interesting statistic, which shows the same trend, is the distribution of driving distance per picked item in the figure to the right. Here, we see that for picking lists with few items, the typical mileage per. item is relatively high (with a large variance, depending on how “lucky” we are with some items being located in the same corridor etc.). For picking lists with several items though, the mileage per. item is gradually decreasing. This type of statistic can thus be interesting to investigate closer, in order to optimize how many items each picking order list should contain in order to minimize the mileage per picked item.

Example 2: Here I have used real-world data that also contains additional information in the form of a customer ID (here shown for only two customers). We can then take a closer look at the distribution in mileage per. picking order list for the two customers. For example, do you typically have to drive longer distances to pick the goods of one customer versus another? And, should you charge that customer extra for this additional cost?
The below figure to the left shows the distribution in mileage for «Customer 1» and «Customer 2» respectively. One of the things we can interpret from this is that for customer 2, most picking order lists have a noticeably shorter driving distance compared to customer 1. This can also be shown by calculating the average mileage per. picking order list for the two customers (figure to the right).

This type of information can e.g. be used to implement pricing models where the product price to the customer is also based on mileage per order. For customers where the order involves more driving (and thus also more time and higher cost) you can consider invoicing extra compared to orders that involve short driving distances.
Summary:
In the end, I hope I have convinced you that graph theory is not just some abstract mathematical concept, but that it actually has many useful and interesting applications! Hopefully, the examples above will be useful for some of you in solving similar problems later, or at least satisfy some of your curiosity when it comes to graph theory and some of its applications.
The cases discussed in the article covers just a few examples that illustrate some of the possibilities that exist. If you have previous experience and ideas on the topic, it would be interesting to hear your thoughts in the comments below!
Did you find the article interesting? If so, you might also like some of my other articles on topics such as AI, Machine Learning, physics, etc., which you can find in the links below and on my medium author profile: https://medium.com/@vflovik
- Deep learning based reverse image search for industrial applications
- Deep Transfer Learning for Image Classification
- Building an AI that can read your mind
- The hidden risk of AI and Big Data
- How to use machine learning for anomaly detection and condition monitoring
- How (not) to use Machine Learning for time series forecasting: Avoiding the pitfalls
- How to use machine learning for production optimization: Using data to improve performance
- How do you teach physics to AI systems?
- Can we build artificial brain networks using nanoscale magnets?
- Artificial Intelligence in Supply Chain Management: Utilizing data to drive operational performance
I also discuss various topics related to AI/machine learning in the workshop presentation below: “ From hype to real-world applications”. I hope you found these resources interesting and useful!
Bio: Vegard Flovik is working on machine learning and advanced analytics at Kongsberg Digital.
Original. Reposted with permission.
Related:
- Graph Representation Learning: The Free eBook
- Building a Deep Learning Based Reverse Image Search
- How (not) to use Machine Learning for time series forecasting: The sequel